题目内容
8．（1）解不等式|x-2|+|x-5|＜5；（2）如果关于x的不等式|x-2|+|x-5|＜a的解集不是空集，求实数a的取值范围．
分析 （1）把要解的不等式等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．
（2）利用绝对值三角不等式，求得|x-2|+|x-5|的最小值，可得实数a的取值范围．
解答 解：（1）不等式|x-2|+|x-5|＜5，
等价于$\left\{\begin{array}{l}{x＜2}\\{2-x+5-x＜5}\end{array}\right.$ ①或，$\left\{\begin{array}{l}{2≤x≤5}\\{x-2+5-x＜5}\end{array}\right.$②，或$\left\{\begin{array}{l}{x＞5}\\{x-2+x-5＜5}\end{array}\right.$③．
解①求得1＜x＜2，解②求得2≤x≤5，解③求得5＜x＜6，
故原不等式的解集为（1，6）．
（2）令y=|x-2|+|x-5|≥|x-2-（x-5）|=3，可得ymin=3，所以a＞3．
点评 本题主要考查绝对值不等式的解法，绝对值三角不等式，函数的恒成立问题，属于中档题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
18．某高校“统计初步”课程的教师为了判断主修统计专业是否与性别有关，随机调查了该选修课的一些学生情况.23名男生中，有10人是统计专业；27名女生中，有20人是统计专业．
（1）根据统计数据填写下面的2×2列联表．
（2）如果判断主修统计专业与性别有关，那么这种判断出错的概率最大不超过多少？
附表：
公式：${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
（1）根据统计数据填写下面的2×2列联表．
| 非统计专业 | 统计专业 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
附表：
| P（k2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
3．函数f（x）=$\frac{x}{2}$-sinx，$x∈（0，\frac{π}{2}）$的单调递减区间是（ ）
| A． | $（0，\frac{π}{6}）$ | B． | $（0，\frac{π}{3}）$ | C． | $（\frac{π}{6}，\frac{π}{2}）$ | D． | $（\frac{π}{3}，\frac{π}{2}）$ |
17．观察下列各式：55=3125，56=15625，57=78125，…，则52016的末四位数字为（ ）
| A． | 3125 | B． | 5625 | C． | 0625 | D． | 8125 |
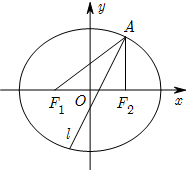已知椭圆E经过点A（2，3），对称轴为坐标轴，焦点F1，F2在x轴上，焦距与长轴长的比为$\frac{1}{2}$．