题目内容
19.(1)若f(x)=|x-1|+|x-4|,求不等式f(x)≥5的解集;(2)若g(x)=|x-1|+|x-a|(a∈R)且?x∈R使得f(x)≤4成立,求a的取值范围.
分析 (1)利用绝对值的意义,分类讨论,即可求不等式f(x)≥5的解集;
(2)由题意?x∈R使得g(x)≤4成立,故g(x)=|x-1|+|x-a|的最小值|a-1|≤4,即可求得a的范围.
解答 解:(1)由题意,x<1,不等式可化为-2x+5≥5,∴x≤0;
1≤x≤4,不等式可化为3≥5,不成立;
x>4,不等式可化为2x-5≥5,∴x≥5;
综上所述不等式的解集为{x|x≤0或x≥5};
(2)由题意?x∈R使得g(x)≤4成立,故g(x)=|x-1|+|x-a|的最小值|a-1|≤4,求得-3≤a≤5.
点评 本题主要考查绝对值的意义.绝对值不等式的解法,函数的能成立问题,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
9.设F1是椭圆${x^2}+\frac{y^2}{4}=1$的下焦点,O为坐标原点,点P在椭圆上,则$\overrightarrow{P{F_1}}•\overrightarrow{PO}$的最大值为( )
| A. | $4+2\sqrt{3}$ | B. | $4-2\sqrt{3}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}+1$ |
10.已知函数f(x)=x3+ax2+bx+a2在x=1处有极值为10,则(a,b)的值( )
| A. | (4,-11) | B. | (-3,3) | C. | (4,-11)或(-3,3) | D. | 不存在 |
4.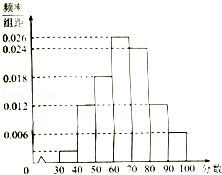 某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ)请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ)请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b=48 | 60 |
| 女生 | c=6 | d=34 | 40 |
| 合计 | 18 | 82 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
9.已知四边形ABCD是菱形,点P在对角线AC上(不包括端点A,C)的充要条件是$\overrightarrow{AP}$=λ($\overrightarrow{AB}$+$\overrightarrow{AD}$),则λ的取值范围( )
| A. | λ∈(0,1) | B. | λ∈(-1,0) | C. | λ∈(0,$\frac{\sqrt{2}}{2}$) | D. | λ∈(-$\frac{\sqrt{2}}{2}$,0) |



