题目内容
20.数列{xn}的前n项和为Sn,且满足:若Sn=$\frac{3}{2}-\frac{1}{2}{x_n}$(x∈N*).(1)求数列{xn}的通项公式;
(2)设数列{an}的各项为正,且满足an≤$\frac{{{x_n}{a_{n-1}}}}{{{x_n}+{a_{n-1}}}}$,a1=1,求证:a1x1+a2x2+a3x3+…+anxn<$\frac{9}{8}$.
分析 (1)利用递推关系即可得出.
(2)${a_n}≤\frac{{{x_n}{a_{n-1}}}}{{{x_n}+{a_{n-1}}}}$,而an>0,xn>0,k可得 $\frac{1}{a_n}≥\frac{1}{x_n}+\frac{1}{{{a_{n-1}}}}\Rightarrow$ $\frac{1}{a_n}-\frac{1}{{{a_{n-1}}}}≥\frac{1}{x_n}$,利用“累加求和”方法可得 $\frac{1}{a_n}-\frac{1}{a_1}≥\frac{1}{x_2}+\frac{1}{x_3}+…+\frac{1}{x_n}$,再利用等比数列的求和公式可得:${a_n}≤\frac{2}{{{3^n}-1}}$.进而得出.
解答 解:(1)由${S_n}=\frac{3}{2}-\frac{1}{2}{x_n}$ …①,得:${S_1}=\frac{3}{2}-\frac{1}{2}{x_1}$,x1=1≠0.
当n≥2 时,${S_{n-1}}=\frac{3}{2}-\frac{1}{2}{x_{n-1}}$ …②,
①-②可得:${x_n}=\frac{1}{3}{x_{n-1}}$ (n≥2 ),∴${x_n}={({\frac{1}{3}})^{n-1}}$.
(2)${a_n}≤\frac{{{x_n}{a_{n-1}}}}{{{x_n}+{a_{n-1}}}}$,而an>0,xn>0,
$\therefore$ $\frac{1}{a_n}≥\frac{1}{x_n}+\frac{1}{{{a_{n-1}}}}\Rightarrow$ $\frac{1}{a_n}-\frac{1}{{{a_{n-1}}}}≥\frac{1}{x_n}$,
$\therefore$ $\frac{1}{a_n}-\frac{1}{a_1}≥\frac{1}{x_2}+\frac{1}{x_3}+…+\frac{1}{x_n}$,
∵a1=1,$\therefore$ $\frac{1}{a_n}≥1+\frac{1}{x_2}+\frac{1}{x_3}+…+\frac{1}{x_n}=1+3+{3^2}+…+{3^{n-1}}=\frac{{{3^n}-1}}{2}$,
$\therefore$ ${a_n}≤\frac{2}{{{3^n}-1}}$.
设Sn=a1x1+a2x2+a3x3+…+anxn,∵${S_n}={a_1}{x_1}+{a_2}{x_2}+{a_3}{x_3}+…+{a_n}{x_n}≤1×1+\frac{2}{8}×\frac{1}{3}+\frac{2}{26}×\frac{1}{9}+…+\frac{2}{{{3^n}-1}}×\frac{1}{{{3^{n-1}}}}$,
当n=1 时,${S_1}=1<\frac{9}{8}$ 当n=2 时,${S_2}≤1+\frac{1}{12}=\frac{13}{12}<\frac{9}{8}$,
当n≥3 时,${a_n}{x_n}≤\frac{2}{{({{3^n}-1}){3^{n-1}}}}<\frac{2}{{{3^{2n-1}}-{3^{n-1}}}}=\frac{2}{{2•{3^{2n-2}}+{3^{2n-2}}-{3^{n-1}}}}<\frac{1}{{{3^{2n-2}}}}$
$\therefore$ ${S_n}<1+\frac{1}{12}+({\frac{1}{9^2}+\frac{1}{9^3}+…+\frac{1}{{{9^{n-1}}}}})=\frac{79}{72}-\frac{1}{{{9^{n-1}}}}<\frac{79}{72}<\frac{9}{8}$.
点评 本题考查了数列的递推关系、“累加求和”、“裂项求和”方法、等比数列的求和公式,考查了推理能力与计算能力,属于难题.

 名校课堂系列答案
名校课堂系列答案| A. | (4,-11) | B. | (-3,3) | C. | (4,-11)或(-3,3) | D. | 不存在 |
| A. | λ∈(0,1) | B. | λ∈(-1,0) | C. | λ∈(0,$\frac{\sqrt{2}}{2}$) | D. | λ∈(-$\frac{\sqrt{2}}{2}$,0) |
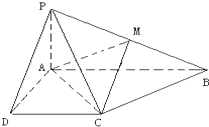 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.