题目内容
16．自然数按下列的规律排列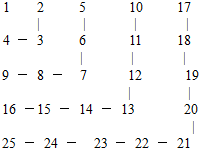
则上起第50行，左起第51列的数为2550．
分析 由题意可知根据数的排列特征，可以从行和列两个角度分析．
解答 解：经观察，这个自然数表的排列特征有：
①第一列的每一个数都是完全平方数，并且恰好等于它所在行数的平方，即第n行的第1个数为n2；
②第一行第n个数为（n-1）2+1；
③第n行中从第1个数至第n个数依次递减1；
④第n列中从第1个数至第n个数依次递增1．
故上起第50行，左起第51列的数，应是第51列的第50个数，
即为[（51-1）2+1]+49=2550，
故答案为：2550．
点评 通过观察数表，由特殊数据来归纳、猜想、证明，进而得出一般规律，较好地考查了同学们阅读理解、获取信息、处理数据、归纳推理等能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．
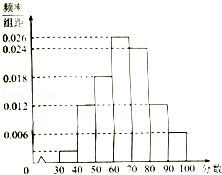某校高二年级共有1600名学生，其中男生960名，女生640名，该校组织了一次满分为100分的数学学业水平模拟考试，根据研究，在正式的学业水平考试中，本次成绩在的学生可取得A等（优秀），在七组加以统计，绘制成频率分布直方图，如图是该频率分布直方图．
（Ⅰ）估计该校高二年级学生在正式的数学学业水平考试中，成绩不合格的人数；
（Ⅱ）请你根据已知条件将下列2×2列联表补充完整，并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”？
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．
某校高二年级共有1600名学生，其中男生960名，女生640名，该校组织了一次满分为100分的数学学业水平模拟考试，根据研究，在正式的学业水平考试中，本次成绩在的学生可取得A等（优秀），在七组加以统计，绘制成频率分布直方图，如图是该频率分布直方图．（Ⅰ）估计该校高二年级学生在正式的数学学业水平考试中，成绩不合格的人数；
（Ⅱ）请你根据已知条件将下列2×2列联表补充完整，并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”？
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b=48 | 60 |
| 女生 | c=6 | d=34 | 40 |
| 合计 | 18 | 82 | n=100 |
| P（k2≥k0） | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
1．不等式2x2-axy+3y2≥0对于任意x∈[1，2]及y∈[1，3]恒成立，则实数a的取值范围是（ ）
| A． | a≤2$\sqrt{2}$ | B． | a≤2$\sqrt{6}$ | C． | a≤5 | D． | a≤$\frac{9}{2}$ |
9．函数y=3sin（$\frac{π}{4}$-3x）+$\sqrt{3}$cos（$\frac{π}{4}$-3x）的最小正周期是（ ）
| A． | $\frac{2π}{3}$ | B． | $\frac{π}{3}$ | C． | 8 | D． | 4 |