题目内容
13.已知函数f(x)=$\frac{1}{2}{x^2}+ax-2{a^2}$lnx(a≠0).(I)讨论函数f(x)的单调性;
(Ⅱ)若f(x)>0恒成立,求a的取值范围.
分析 (I)先求出函数的定义域,进而根据函数的解析式,求出函数的导函数,分析导函数符号在不同区间上的取值,根据导函数符号与原函数的单调性之间的关系可得结论;
(II)若f(x)>0恒成立,则f(x)的最小值大于0,根据(I)中结论,求出函数的最小值,代入构造关于a的不等式,解不等式可得a的取值范围
解答 解:(I)f(x)的定义域为(0,+∞),$f'(x)=x+a-\frac{{2{a^2}}}{x}=\frac{{{x^2}+ax-2{a^2}}}{x}=\frac{{({x+2a})({x-a})}}{x}$
(1)当a<0时,在(0,-2a)上f'(x)<0,在(-2a,+∞)上f'(x)>0.
因此,f(x)在(0,-2a)上递减,在(-2a,+∞)上递增.
(2)当a>0时,在(0,a)上f'(x)<0,在(a,+∞)上f'(x)>0.
因此,f(x)在(0,a)上递减,在(a,+∞)上递增.
(II)由(I)知:a<0时,$f{(x)_{min}}=f({-2a})=2{a^2}-2{a^2}-2{a^2}ln({-2a})=-2{a^2}ln({-2a})$
由f(x)>0得:$ln({-2a})<0⇒0<-2a<1⇒-\frac{1}{2}<a<0$,
当a>0时,$f{(x)_{min}}=f(a)=\frac{1}{2}{a^2}+{a^2}-2{a^2}lna=\frac{3}{2}{a^2}-2{a^2}lna$
由f(x)>0得:$\frac{3}{2}{a^2}-2{a^2}lna>0⇒lna<\frac{3}{4}⇒0<a<{e^{\frac{3}{4}}}$
综上得:$a∈({-\frac{1}{2},0})∪({0,{e^{\frac{3}{4}}}})$.
点评 本题考查的知识点是利用导数求函数的单调区间和最值,其中熟练掌握参数的处理方法与技巧,是解答的关键,属于中档题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
| A. | $\frac{80}{\begin{array}{l}3\end{array}}$ | B. | $\frac{40}{\begin{array}{l}3\end{array}}$ | C. | 80 | D. | 40 |
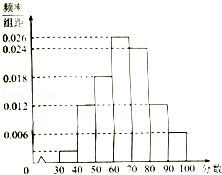 某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.
某校高二年级共有1600名学生,其中男生960名,女生640名,该校组织了一次满分为100分的数学学业水平模拟考试,根据研究,在正式的学业水平考试中,本次成绩在的学生可取得A等(优秀),在七组加以统计,绘制成频率分布直方图,如图是该频率分布直方图.(Ⅰ)估计该校高二年级学生在正式的数学学业水平考试中,成绩不合格的人数;
(Ⅱ)请你根据已知条件将下列2×2列联表补充完整,并判断是否有90%的把握认为“该校高二年级学生在本次考试中数学成绩优秀与性别有关”?
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 男生 | a=12 | b=48 | 60 |
| 女生 | c=6 | d=34 | 40 |
| 合计 | 18 | 82 | n=100 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
| A. | a≤2$\sqrt{2}$ | B. | a≤2$\sqrt{6}$ | C. | a≤5 | D. | a≤$\frac{9}{2}$ |
| A. | 产量每增加1000件,单位成本下降2.13元 | |
| B. | 产量每减少1000件,单位成本下降2.13元 | |
| C. | 产量每增加1000件,单位成本上升2130元 | |
| D. | 产量每减少1000件,单位成本上升2130元 |