题目内容
设抛物线y2=4x的焦点为F，准线为l，A为抛物线上一点，AK⊥l，K为垂足，如果直线KF的斜率为-1，则△AKF的面积为 ．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：求出直线KF的方程，可得A的坐标，即可求出△AKF的面积．
解答：
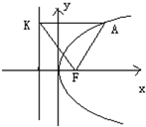解：由题意F（1，0），直线KF的方程为y=-x+1，
当x=-1时，y=2，
∴A（1，2），
∴底边长AK=2，高为2，
∴△AKF的面积为
•2•2=2．
故答案为：2．
解：由题意F（1，0），直线KF的方程为y=-x+1，当x=-1时，y=2，
∴A（1，2），
∴底边长AK=2，高为2，
∴△AKF的面积为
| 1 |
| 2 |
故答案为：2．
点评：本题考查△AKF的面积，考查抛物线的性质，确定A的坐标是关键．
练习册系列答案
应用题作业本系列答案
相关题目
用一平面去截球所得截面的面积为3πcm2，已知球心到该截面的距离为1cm，则该球的体积是0＜x＜3是|x-1|＜2成立的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |