题目内容
已知函数f(x)=ksin(ωx+φ),(k>0,ω>0,|φ|<
)的一系列对应值如下表:
(1)根据表格提供的数据求函数f(x)的解析式;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,根据(1)的结果,若f(
)=-1,且a=2,求b+c的取值范围.
| π |
| 2 |
| x | -
|
|
|
|
|
|
| ||||||||||||||
| y | -2 | 0 | 2 | 0 | -2 | 0 | 2 |
(2)设△ABC的内角A,B,C的对边分别为a,b,c,根据(1)的结果,若f(
| A |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由函数的最值求出A,由周期求出ω,把特殊点的坐标代入函数的解析式求出φ的值,可得函数的解析式.
(2)由f(
)=-1,求得A=
.再由a=2,利用正弦定理可得 b=
sinB,c=
sinC,再根据b+c=
(sinB+sinC)=4cos(B-
).再结合B∈(0,
),利用余弦函数的定义域和值域求得b+c的范围.
(2)由f(
| A |
| 2 |
| π |
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
| π |
| 3 |
| 2π |
| 3 |
解答:
解:(1)由条件可得k=2,再根据周期为T=
=
+
=2π,∴ω=1.
再把点(-
,-2)代入函数的解析式可得 2sin(-
+φ)=-2,
令-
+φ=2kπ-
,k∈z,可得 φ=2kπ-
,结合,|φ|<
,可得φ=-
,
∴f(x)=2sin(x-
).
(2)∵f(
)=2sin(
-
)=-1,∴sin(
-
)=-
,结合A∈(0,π),可得A=
.
再由a=2,利用正弦定理可得
=
=
,即
=
=
,
可得 b=
sinB,c=
sinC,∴b+c=
(sinB+sinC)=
(sinB+sin(
-B)),
=
•2sin
cos(B-
)=4cos(B-
).
∵B∈(0,
),∴B-
∈(-
,
),∴cos(B-
)∈(
,1],
∴4cos(B-
)∈(2,4],即b+c∈(2,4].
| 2π |
| ω |
| 11π |
| 6 |
| π |
| 6 |
再把点(-
| π |
| 6 |
| π |
| 6 |
令-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
∴f(x)=2sin(x-
| π |
| 3 |
(2)∵f(
| A |
| 2 |
| A |
| 2 |
| π |
| 3 |
| A |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
再由a=2,利用正弦定理可得
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| 2 | ||||
|
| b |
| sinB |
| c |
| sinC |
可得 b=
4
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
| 2π |
| 3 |
=
4
| ||
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∵B∈(0,
| 2π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴4cos(B-
| π |
| 3 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,两角和的正弦公式、正弦定理、余弦函数的定义域和值域,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
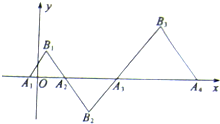 如图,在直角坐标平面xOy中,△AjBjAj+1(其中j=1,2,n,…)为正三角形,且满足
如图,在直角坐标平面xOy中,△AjBjAj+1(其中j=1,2,n,…)为正三角形,且满足