题目内容
已知集合A={x|-3＜x≤5}，集合B={y|-2＜y＜7}，求A∩B、A∪B、（∁RA）∩B．
考点：交、并、补集的混合运算
专题：集合
分析：利用集合的交并补的定义求集合A∩B、A∪B，在求解（∁RA）∩B时，可以先求∁RA．
解答：
解：集合A={x|-3＜x≤5}，集合B={y|-2＜y＜7}，
则A∩B={x|-3＜x≤5}∩{y|-2＜y＜7}=（-2，5]，
A∪B={x|-3＜x≤5}∪{y|-2＜y＜7}=（-3，7），
∵∁RA=（-∞，3]∪（5，+∞），
∴（∁RA）∩B=（-∞，-3]∪（5，+∞）∩（-2，7）=（5，7）．
则A∩B={x|-3＜x≤5}∩{y|-2＜y＜7}=（-2，5]，
A∪B={x|-3＜x≤5}∪{y|-2＜y＜7}=（-3，7），
∵∁RA=（-∞，3]∪（5，+∞），
∴（∁RA）∩B=（-∞，-3]∪（5，+∞）∩（-2，7）=（5，7）．
点评：本题集合的混合运算，属于基础题目，较简单，要熟练集合的交并补定义．
练习册系列答案
小学期末标准试卷系列答案
相关题目
设f（x-2）=2x，则f（3）的值为（ ）
| A、64 | B、8 | C、16 | D、32 |
如果命题“p且q”是假命题，“非p”是真命题，那么（ ）
| A、命题p一定是真命题 |
| B、命题q一定是真命题 |
| C、命题q一定是假命题 |
| D、命题q可以是真命题也可以是假命题 |
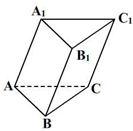斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧棱长等于b，一条侧棱AA1与底面相邻两边AB、AC都成45°角，求这个三棱柱的侧面积．在数列{an}中，a1=1，an+1=2an（n∈N*），则a10=（ ）
| A、19 |
| B、21 |
| C、29 |
| D、210 |
函数f（x）=
的值域（ ）
|
| A、[-9，+∞） | ||
B、[-9，0]∪(0，
| ||
C、[-9，0]∪[
| ||
D、[-8，0]∪[
|