Question

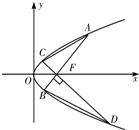已知点F是抛物线y²=2px的焦点，其中p是正常数，AB，CD都是抛物线经过点F的弦，且AB⊥CD，AB的斜率为k，且k＞0，C，A两点在x轴上方．
（1）求

1

|AB|

+

1

|CD|

；
（2）①当|AF|•|BF|=

4

3

p²时，求k；
②设△AFC与△BFD的面积之和为S，求当k变化时S的最小值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）设A(x1，y1)，B(x2，y2)，AB：y=k(x-

p

2

)，由

y2=2px y=k(x- p 2 )

，得k2x2-p(k2+2)x+

1

4

k2p2=0，由此利用韦达定理、抛物线定义，结合已知条件得

1

|AB|

+

1

|CD|

=

1

2p

．
（2）①|AF|•|BF|=(x1+

p

2

)(x2+

p

2

)=x1x2+

p

2

(x1+x2)+

p2

4

=

p2

2

+

k2+2

k2

•

p2

2

=

k2+1

k2

•p2，由此能求出k=

3

．
②由|CF|•|DF|=（k²+1）p²，|AF|•|BF|=

k2+1

k2

•p2，能求出当k=1时，S有最小值2p²．

解答： 解：（1）设A(x1，y1)，B(x2，y2)，AB：y=k(x-

p

2

)
由

y2=2px y=k(x- p 2 )

，得k2x2-p(k2+2)x+

1

4

k2p2=0，
由韦达定理，得：x1+x2=

k2+2

k2

p，x1•x2=

p2

4

…（2分）
由抛物线定义得|AB|=|AF|+|BF|=x1+x2+p=

k2+1

k2

2p
同理，用-

1

k

换k，得|CD|=(k2+1)2p，
∴

1

|AB|

+

1

|CD|

=

1

2p

．…（5分）
（2）①|AF|•|BF|=(x1+

p

2

)(x2+

p

2

)=x1x2+

p

2

(x1+x2)+

p2

4

=

p2

2

+

k2+2

k2

•

p2

2

=

k2+1

k2

•p2…（8分）
当|AF|•|BF|=

4

3

p2时，

k2+1

k2

•p2=

4

3

p2，
又k＞0，解得k=

3

…（9分）
②由①同理知|CF|•|DF|=（k²+1）p²，
|AF|•|BF|=

k2+1

k2

•p2，
由变形得|BF|=

k2+1

k2

p2

|AF|

，|CF|=

(k2+1)•p2

|DF|

，…（10分）
又AB⊥CD，
∴S=

1

2

|AF|•|CF|+

1

2

|BF|•|DF|=

1

2

[

|AF|

|DF|

(k2+1)+

|DF|

|AF|

k2+1

k2

]p2…（12分）≥

(k2+1)(1+ 1 k2 )

p2≥

2k 2 k

p2=2p2
∴当k=1时，S有最小值2p²…（14分）

点评：本题考查

1

|AB|

+

1

|CD|

的求法，考查直线斜率的求法，考查两个三角形的面积之和的最小值的求法，解题时要认真审题，注意函数与方程思想的合理运用．