题目内容
在△ABC中,A是锐角,且
b=2asinB.
(Ⅰ)求角A的大小;
(Ⅱ)若a=7,△ABC的面积为10
,求b2+c2的值.
| 3 |
(Ⅰ)求角A的大小;
(Ⅱ)若a=7,△ABC的面积为10
| 3 |
考点:余弦定理,正弦定理
专题:解三角形
分析:(Ⅰ)已知等式利用正弦定理化简,由sinB不为0求出sinA的值,即可确定出角A的大小;
(Ⅱ)由sinA,已知三角形面积,利用三角形面积公式求出bc的值,利用余弦定理列出关系式,把a,cosA,bc的值代入求出b2+c2的值即可.
(Ⅱ)由sinA,已知三角形面积,利用三角形面积公式求出bc的值,利用余弦定理列出关系式,把a,cosA,bc的值代入求出b2+c2的值即可.
解答:
解:(Ⅰ)已知等式
b=2asinB,利用正弦定理化简得:
sinB=2sinAsinB,
∵sinB≠0,∴sinA=
,
∵A为锐角,
∴A=60°;
(Ⅱ)∵sinA=
,△ABC面积为10
,
∴
bcsinA=10
,即bc=40,
∵a=7,cosA=
,
∴由余弦定理得:a2=b2+c2-2bccosA,即49=b2+c2+bc=b2+c2+40,
整理得:b2+c2=9.
| 3 |
| 3 |
∵sinB≠0,∴sinA=
| ||
| 2 |
∵A为锐角,
∴A=60°;
(Ⅱ)∵sinA=
| ||
| 2 |
| 3 |
∴
| 1 |
| 2 |
| 3 |
∵a=7,cosA=
| 1 |
| 2 |
∴由余弦定理得:a2=b2+c2-2bccosA,即49=b2+c2+bc=b2+c2+40,
整理得:b2+c2=9.
点评:此题考查了正弦、余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知函数f(x)在x=1处的导数为2,则
的值为( )
| lim |
| h→0 |
| f(1-h)-f(1+h) |
| h |
| A、-4 | B、-1 | C、4 | D、1 |
函数f(x)=x•cosx是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数也不是偶函数 |
cos(-
π)等于( )
| 23 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若f(x)=
,则f[f(2)]=( )
|
| A、0 | B、1 | C、-1 | D、2 |
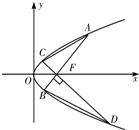 已知点F是抛物线y2=2px的焦点,其中p是正常数,AB,CD都是抛物线经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,C,A两点在x轴上方.
已知点F是抛物线y2=2px的焦点,其中p是正常数,AB,CD都是抛物线经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,C,A两点在x轴上方.