题目内容
求函数f（x）=2x3-3x2-12x+5的极大值和极小值．
考点：利用导数研究函数的极值
专题：计算题,导数的综合应用
分析：求导f′（x）=6x2-6x-12=6（x+1）（x-2），从而确定函数的单调性与极值．
解答：
解：∵f（x）=2x3-3x2-12x+5，
∴f′（x）=6x2-6x-12=6（x+1）（x-2）；
故当x＞2或x＜-1时，f′（x）＞0，
当-1＜x＜2时，f′（x）＜0；
故f（x）在（-∞，-1），（2，+∞）上是增函数，
在（-1，2）上是减函数；
故f（x）在x=-1处有极大值f（-1）=12，
f（x）在x=2处有极小值f（2）=-15．
∴f′（x）=6x2-6x-12=6（x+1）（x-2）；
故当x＞2或x＜-1时，f′（x）＞0，
当-1＜x＜2时，f′（x）＜0；
故f（x）在（-∞，-1），（2，+∞）上是增函数，
在（-1，2）上是减函数；
故f（x）在x=-1处有极大值f（-1）=12，
f（x）在x=2处有极小值f（2）=-15．
点评：本题考查了导数的综合应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
函数f（x）=x•cosx是（ ）
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数也不是偶函数 |
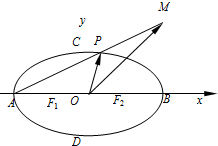如图，在直角坐标系xOy中，椭圆
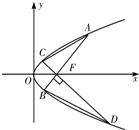已知点F是抛物线y2=2px的焦点，其中p是正常数，AB，CD都是抛物线经过点F的弦，且AB⊥CD，AB的斜率为k，且k＞0，C，A两点在x轴上方．
如图，已知圆G：x2-x+y2=0，经过抛物线y2=2px的焦点，过点（m，0）（m＜0）倾斜角为