题目内容
某人造卫星在地球赤道平面绕地球飞行,甲、乙两个监测点分别位于赤道上东经131°和147°,在某时刻测得甲监测点到卫星的距离为1537.45 千米,乙监测点到卫星的距离为887.64 千米.假设地球赤道是一个半径为6378千米的圆,求此时卫星所在位置的高度(结果精确到0.01 千米)和经度(结果精确到0.01°).
考点:球面距离及相关计算
专题:解三角形
分析:设地球球心为O,甲、乙两个监测点分别为A,B,卫星位置为C,则O,A,B,C四点均在赤道面上,进而利用余弦定理解△OAB,△ABC,△OAC可得答案.
解答:
解:设地球球心为O,甲、乙两个监测点分别为A,B,卫星位置为C,
则O,A,B,C四点均在赤道面上,如下图所示:
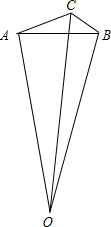
故OA=OB=6378,AC=1537.45,BC=887.64,
在△OAB中,∠AOB=147°-131°=16°,
故∠OAB=∠OBA=82°,
故AB=
≈1875.50,
在△ABC中,cos∠CAB=
≈0.8832,
故∠CAB≈28°,
在△AOC中,∠CAO=110°,
故OC=
≈7098.61,
∵7098.61-6378=720.61,
故卫星所在位置的高度约为720.61千米;
cos∠AOC=
≈0.9796,
∴∠AOC≈11.6°,
由131°+11.6°=142.6°,
故卫星所在位置的经度约为142.6°.
则O,A,B,C四点均在赤道面上,如下图所示:

故OA=OB=6378,AC=1537.45,BC=887.64,
在△OAB中,∠AOB=147°-131°=16°,
故∠OAB=∠OBA=82°,
故AB=
| 63782+63782-2•63782•cos16° |
在△ABC中,cos∠CAB=
| 1537.452+1875.502-887.642 |
| 2×1537.45×1875.50 |
故∠CAB≈28°,
在△AOC中,∠CAO=110°,
故OC=
| 63782+1537.452-2•6378•1537.45 •cos110° |
∵7098.61-6378=720.61,
故卫星所在位置的高度约为720.61千米;
cos∠AOC=
| 63782+71098.612-1537.452 |
| 2×6378×71098.61 |
∴∠AOC≈11.6°,
由131°+11.6°=142.6°,
故卫星所在位置的经度约为142.6°.
点评:本题考查的知识点余弦定理,但本题所涉及的数据计算起来太复杂,故不建议运算,只了解运算思路即可.

练习册系列答案
相关题目
若f(x)=
,则f[f(2)]=( )
|
| A、0 | B、1 | C、-1 | D、2 |
 已知点F是抛物线y2=2px的焦点,其中p是正常数,AB,CD都是抛物线经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,C,A两点在x轴上方.
已知点F是抛物线y2=2px的焦点,其中p是正常数,AB,CD都是抛物线经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,C,A两点在x轴上方. 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4.点M,N分别是AA1,AB的中点,则异面直线CM与D1N所成角的余弦值为
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4.点M,N分别是AA1,AB的中点,则异面直线CM与D1N所成角的余弦值为