题目内容
已知曲线C:
+
=1,直线l:
(t为参数)
(1)写出曲线C的参数方程,直线l的普通方程;
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
| x2 |
| 4 |
| y2 |
| 9 |
|
(1)写出曲线C的参数方程,直线l的普通方程;
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
考点:直线的参数方程,三角函数的最值
专题:坐标系和参数方程
分析:(1)由平方关系和曲线C方程写出曲线C的参数方程,消去参数t即可得直线l的普通方程;
(2)由曲线C的参数方程设曲线C上任意一点P的坐标,利用点到直线的距离公式求出点P直线l的距离,利用正弦函数求出|PA|,利用辅助角公式进行化简,再由正弦函数的性质求出|PA|的最大值与最小值.
(2)由曲线C的参数方程设曲线C上任意一点P的坐标,利用点到直线的距离公式求出点P直线l的距离,利用正弦函数求出|PA|,利用辅助角公式进行化简,再由正弦函数的性质求出|PA|的最大值与最小值.
解答:
解:(1)由题意得,曲线C:
+
=1,
所以曲线C的参数方程为
(θ为参数),
因为直线l:
(t为参数),
所以直线l的普通方程为2x+y-6=0 …(5分)
(2)曲线C上任意一点P(2cosθ,3sinθ),
则点P直线l的距离为d=
=
,
则|PA|=
=
|4cosθ+3sinθ-6|=
|5sin(θ+α)-6|(其中α为锐角且tanα=
),
当sin(θ+α)=-1时,|PA|取得最大值,最大值为
,
当sin(θ+α)=1时,|PA|取得最小值,最小值为
…(10分)
| x2 |
| 4 |
| y2 |
| 9 |
所以曲线C的参数方程为
|
因为直线l:
|
所以直线l的普通方程为2x+y-6=0 …(5分)
(2)曲线C上任意一点P(2cosθ,3sinθ),
则点P直线l的距离为d=
| |4cosθ+3sinθ-6| | ||
|
| ||
| 5 |
则|PA|=
| d |
| sin30° |
2
| ||
| 5 |
2
| ||
| 5 |
| 4 |
| 3 |
当sin(θ+α)=-1时,|PA|取得最大值,最大值为
22
| ||
| 5 |
当sin(θ+α)=1时,|PA|取得最小值,最小值为
2
| ||
| 5 |
点评:本题考查参数方程与普通方程互化,点到直线的距离公式,以及辅助角公式、正弦函数的性质等,比较综合,熟练掌握公式是解题的关键.

练习册系列答案
相关题目
cos(-
π)等于( )
| 23 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知全集U=R,集合A=(x|-1<x<2},集合B={x|x<-2或x>1},则∁U(A∪B)等于( )
| A、{x|-2<x<-1} |
| B、{x|-2≤x≤-1} |
| C、{x|x<-2或x>-1} |
| D、{x|x≤-2或x≥-1} |
若一条直线与一个平面成72°角,则这条直线与这个平面内经过斜足的直线所成角中最大角等于( )
| A、72° | B、90° |
| C、108° | D、180° |
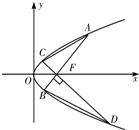 已知点F是抛物线y2=2px的焦点,其中p是正常数,AB,CD都是抛物线经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,C,A两点在x轴上方.
已知点F是抛物线y2=2px的焦点,其中p是正常数,AB,CD都是抛物线经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,C,A两点在x轴上方. 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4.点M,N分别是AA1,AB的中点,则异面直线CM与D1N所成角的余弦值为
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4.点M,N分别是AA1,AB的中点,则异面直线CM与D1N所成角的余弦值为