题目内容
命题“?x∈R,x2-2ax+3>0”是真命题,实数a的取值范围是 .
考点:全称命题
专题:简易逻辑
分析:根据全称命题的性质即可得到结论.
解答:
解:命题“?x∈R,x2-2ax+3>0”是真命题,
则判别式△=4a2-4×3<0,
故a2<3,
即-
<a<
,
故答案为:-
<a<
则判别式△=4a2-4×3<0,
故a2<3,
即-
| 3 |
| 3 |
故答案为:-
| 3 |
| 3 |
点评:本题主要考查全称命题的应用,根据不等式恒成立和判别式△的关系是解决本题的关键.

练习册系列答案
相关题目
cos(-
π)等于( )
| 23 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若f(x)=
,则f[f(2)]=( )
|
| A、0 | B、1 | C、-1 | D、2 |
已知全集U=R,集合A=(x|-1<x<2},集合B={x|x<-2或x>1},则∁U(A∪B)等于( )
| A、{x|-2<x<-1} |
| B、{x|-2≤x≤-1} |
| C、{x|x<-2或x>-1} |
| D、{x|x≤-2或x≥-1} |
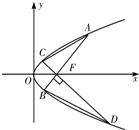 已知点F是抛物线y2=2px的焦点,其中p是正常数,AB,CD都是抛物线经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,C,A两点在x轴上方.
已知点F是抛物线y2=2px的焦点,其中p是正常数,AB,CD都是抛物线经过点F的弦,且AB⊥CD,AB的斜率为k,且k>0,C,A两点在x轴上方. 如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4.点M,N分别是AA1,AB的中点,则异面直线CM与D1N所成角的余弦值为
如图,长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=4.点M,N分别是AA1,AB的中点,则异面直线CM与D1N所成角的余弦值为