题目内容
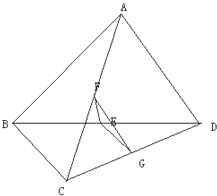
空间四边形ABCD中,E、F分别为对角线BD、AC中点,若BC=AD=2EF,求直线EF与AD所成的角.

考点:异面直线及其所成的角
专题:空间角
分析:取CD的中点G,连接FG,EG,又F为AC的中点.利用三角形的中位线定理可得FG
AD,因此∠EFG即为异面直线EF与AD所成的角或其补角.同理可得EG=
BC.
可得△EFG为等边三角形.进而得出.
| ∥ |
. |
| 1 |
| 2 |
| 1 |
| 2 |
可得△EFG为等边三角形.进而得出.
解答:
解:如图所示,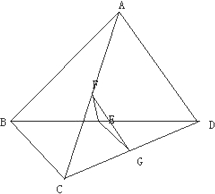
取CD的中点G,连接FG,EG,又F为AC的中点.
则FG
AD,
∴∠EFG即为异面直线EF与AD所成的角或其补角.
∵E为BD的中点,同理可得EG=
BC.
∵BC=AD=2EF,
∴EF=FG=EG.
∴△EFG为等边三角形.
∴∠EFG=60°.
即异面直线EF与AD所成的角为60°.

取CD的中点G,连接FG,EG,又F为AC的中点.
则FG
| ∥ |
. |
| 1 |
| 2 |
∴∠EFG即为异面直线EF与AD所成的角或其补角.
∵E为BD的中点,同理可得EG=
| 1 |
| 2 |
∵BC=AD=2EF,
∴EF=FG=EG.
∴△EFG为等边三角形.
∴∠EFG=60°.
即异面直线EF与AD所成的角为60°.
点评:本题考查了异面直线所成的夹角、三角形的中位线定理、等边三角形的定义及其性质,考查了推理能力和计算能力,考查了空间想象能力.

练习册系列答案
相关题目
函数f(x)=x3-ax在(-∞,1]上递增,则a的范围是( )
| A、a>3 | B、a≥3 |
| C、a<3 | D、a≤3 |