题目内容
8.已知函数f(x)=x3-ax在x=1处取得极小值,其中a是实数.(1)求实数a的值;
(2)用反证法证明:当x>0时,$-\frac{2f(x)}{x^2}$,$\frac{f'(x)}{x}$中至少有一个不小于$\sqrt{3}$.
分析 (1)求出函数的导数,根据f′(1)=0,求出a的值即可;
(2)假设$-\frac{2f(x)}{x^2}$,$\frac{f'(x)}{x}$都小于$\sqrt{3}$,得到关于x的不等式组,得出矛盾,证出结论即可.
解答 解:(1)∵f(x)=x3-ax,
∴f'(x)=3x2-a,…(2分)
∵函数f(x)=x3-ax在x=1处取得极小值,
∴f'(1)=0,…(5分)
即3-a=0,
∴a=3. …(7分)
证明:(2)假设$-\frac{2f(x)}{x^2}$,$\frac{f'(x)}{x}$都小于$\sqrt{3}$
即$\left\{{\begin{array}{l}{-\frac{2f(x)}{x^2}<\sqrt{3}}\\{\frac{f'(x)}{x}<\sqrt{3}}\end{array}}\right.$…(9分)
∴$\left\{{\begin{array}{l}{-2x+\frac{6}{x}<\sqrt{3}}\\{3x-\frac{3}{x}<\sqrt{3}}\end{array}}\right.$
∴$(-2x+\frac{6}{x})+(3x-\frac{3}{x})<2\sqrt{3}$,…(11分)
即$x+\frac{3}{x}<2\sqrt{3}$,
当x>0时,$x+\frac{3}{x}≥2\sqrt{x•\frac{3}{x}}=2\sqrt{3}$,当且仅当$x=\frac{3}{x}$,即$x=\sqrt{3}$时等号成立,
∴假设不成立,
∴$-\frac{2f(x)}{x^2}$,$\frac{f'(x)}{x}$中至少有一个不小于$\sqrt{3}$…(14分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及反证法的应用,是一道中档题.

| A. | 109 | B. | 99 | C. | $\frac{99}{2}$ | D. | $\frac{109}{2}$ |
| A. | 三点唯一确定一个平面 | |
| B. | 一条直线和一个点唯一确定一个平面 | |
| C. | 两条平行线与同一条直线相交,三条直线在同一平面内 | |
| D. | 空间两两相交的三条直线在同一平面内 |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |
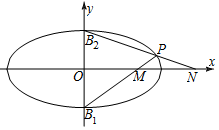 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴两端点为B1(0,-1)、B2(0,1),离心率e=$\frac{\sqrt{3}}{2}$,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴两端点为B1(0,-1)、B2(0,1),离心率e=$\frac{\sqrt{3}}{2}$,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,