题目内容
16.已知m∈R,命题p:复数z=(m-2)+mi(i是虚数单位)在复平面内对应的点在第二象限,命题q:复数z=(m-2)+mi的模不大于$\sqrt{10}$.(1)若p为真命题,求m的取值范围;
(2)若命题¬p,命题q都为真,求m的取值范围.
分析 (1)根据复数的几何意义结合命题的真假关系进行求解即可.
(2)求出命题q的等价条件,建立不等式关系进行求解即可.
解答 解:(1)复数z=(m-2)+mi(i是虚数单位)在复平面内对应的点在第二象限,
则$\left\{\begin{array}{l}{m-2<0}\\{m>0}\end{array}\right.$得0<m<2,即若p为真命题,则0<m<2.
(2)命题q:复数z=(m-2)+mi的模不大于$\sqrt{10}$,则|z|=$\sqrt{(m-2)^{2}+{m}^{2}}$≤$\sqrt{10}$,即m2-2m-3≤0,得-1≤m≤3,即q:-1≤m≤3,
若命题¬p,命题q都为真,
则$\left\{\begin{array}{l}{m≥2或m≤0}\\{-1≤m≤3}\end{array}\right.$,
即-1≤m≤0或2≤m≤3.
点评 本题主要考查复数的几何意义以及命题真假关系的应用.考查学生的转化意识.

练习册系列答案
相关题目
6.斜率为1的直线与抛物线y=ax2(a>0)交于A、B两点,且线段AB的中点C到y轴的距离为1,则该抛物线焦点到准线的距离为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
7.设m∈R,命题“若m≥0,则方程x2=m有实根”的逆否命题是( )
| A. | 若方程x2=m有实根,则m≥0 | B. | 若方程x2=m有实根,则m<0 | ||
| C. | 若方程x2=m没有实根,则m≥0 | D. | 若方程x2=m没有实根,则m<0 |
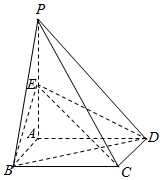 如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥底面ABCD,E是PA的中点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PA⊥底面ABCD,E是PA的中点. 如图,某几何体的三视图中,正视图和侧视图都是半径为$\sqrt{3}$的半圆和相同的正三角形,其中三角形的上顶点是半圆的中点,底边在直径上,则它的表面积是( )
如图,某几何体的三视图中,正视图和侧视图都是半径为$\sqrt{3}$的半圆和相同的正三角形,其中三角形的上顶点是半圆的中点,底边在直径上,则它的表面积是( )