题目内容
 如图,已知椭圆C1:
如图,已知椭圆C1:| x2 |
| 8 |
| y2 |
| 4 |
| x2 |
| 4 |
| y2 |
| 4 |
为双曲线上异于顶点的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
(Ⅰ)设直线PF1、PF2的斜率分别为k1、k2,求:k1•k2的值;
(Ⅱ)是否存在常数λ,使得|AB|+|CD|=λ|AB|•|CD|恒成立?若存在,求λ的值;若不存在,请说明理由.
考点:圆锥曲线的综合
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)求出直线PF1、PF2的斜率,利用P为双曲线
-
=1上异于顶点的任意一点,化简即可得出结论.
(Ⅱ)问题等价于
+
=λ,即
+
是否是定值问题,利用韦达定理求得弦长,化简,即可得到结论.
| x2 |
| 4 |
| y2 |
| 4 |
(Ⅱ)问题等价于
| 1 |
| |AB| |
| 1 |
| |CD| |
| 1 |
| |AB| |
| 1 |
| |CD| |
解答:
解:(Ⅰ)设A(x1,y1),B(x2,y2),P(x0,y0),则k1=
,k2=
.
∵P为双曲线
-
=1上异于顶点的任意一点,
∴x02-y02=4,
∴k1k2=
•
=
=1,即k1•k2=1;
(Ⅱ)由于直线PF1的方程是y=k1(x+2),代入椭圆方程并整理得(1+2k12)x2+8k12x+8k12-8=0.
∴x1+x2=-
,x1x2=
∴|AB|=
•
=4
•
同理可得|CD|=4
•
.
则
+
=
•(
+
)
又k1k2=1
∴
+
=
(
+
)=
故|AB|+|CD|=
|AB|•|CD|
因此,存在λ=
,使|AB|+|CD|=λ|AB|•|CD|恒成立.
| y0 |
| x0+2 |
| y0 |
| x0-2 |
∵P为双曲线
| x2 |
| 4 |
| y2 |
| 4 |
∴x02-y02=4,
∴k1k2=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
| y02 |
| x02-4 |
(Ⅱ)由于直线PF1的方程是y=k1(x+2),代入椭圆方程并整理得(1+2k12)x2+8k12x+8k12-8=0.
∴x1+x2=-
| 8k12 |
| 2k12+1 |
| 8k12-8 |
| 2k12+1 |
∴|AB|=
| 1+k12 |
| (x1+x2)2-4x1x2 |
| 2 |
| k12+1 |
| 2k12+1 |
同理可得|CD|=4
| 2 |
| k22+1 |
| 2k22+1 |
则
| 1 |
| |AB| |
| 1 |
| |CD| |
| 1 | ||
4
|
| 2k12+1 |
| k12+1 |
| 2k22+1 |
| k22+1 |
又k1k2=1
∴
| 1 |
| |AB| |
| 1 |
| |CD| |
| 1 | ||
4
|
| 2k12+1 |
| k12+1 |
| k12+2 |
| k12+1 |
3
| ||
| 8 |
故|AB|+|CD|=
3
| ||
| 8 |
因此,存在λ=
3
| ||
| 8 |
点评:本题考查椭圆的几何性质,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
设函数f(x)=x2+
-a(x≠0),a为常数且a>2,则f(x)的零点个数是( )
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
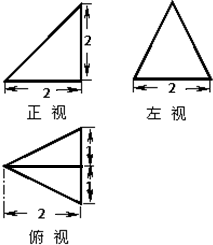 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知△ABC内一点O满足关系式2
+
+3
=
,则△AOC的面积与△ABC的面积之比为( )
| OA |
| OB |
| OC |
| 0 |
| A、1:6 | B、1:3 |
| C、1:2 | D、5:6 |
设a是函数f(x)=|x2-4|-lnx在定义域内的最小零点,若0<x0<a,则f(x0)的值满足( )
| A、f(x0)>0 |
| B、f(x0)<0 |
| C、f(x0)=0 |
| D、f(x0)的符号不确定 |