题目内容
已知函数f(x)=x2+1,g(x)=4x+1,的定义域都是集合A,函数f(x)和g(x)的值域分别为S和T,
①若A=[1,2],求S∩T
②若A=[0,m]且S=T,求实数m的值
③若对于集合A的任意一个数x的值都有f(x)=g(x),求集合A.
①若A=[1,2],求S∩T
②若A=[0,m]且S=T,求实数m的值
③若对于集合A的任意一个数x的值都有f(x)=g(x),求集合A.
考点:集合的包含关系判断及应用
专题:函数的性质及应用
分析:①根据函数的定义域分别求出两个奇函数的值域,根据集合的基本运算求S∩T.
②根据条件A=[0,m]且S=T,建立条件关系即可求实数m的值.
③根据条件f(x)=g(x)建立条件关系即可求集合A.
②根据条件A=[0,m]且S=T,建立条件关系即可求实数m的值.
③根据条件f(x)=g(x)建立条件关系即可求集合A.
解答:
解:(1)若A=[1,2],
则函数f(x)=x2+1的值域是S=[2,5],
g(x)=4x+1的值域T=[5,9],
∴S∩T={5}.
(2)若A=[0,m],则S=[1,m2+1],T=[1,4m+1],
由S=T得m2+1=4m+1,解得m=4或m=0(舍去).
(3)若对于A中的每一个x值,都有f(x)=g(x),
即x2+1=4x+1,
∴x2=4x,
解得x=4或x=0,
∴满足题意的集合是{0],或{4}或{0,4}.
则函数f(x)=x2+1的值域是S=[2,5],
g(x)=4x+1的值域T=[5,9],
∴S∩T={5}.
(2)若A=[0,m],则S=[1,m2+1],T=[1,4m+1],
由S=T得m2+1=4m+1,解得m=4或m=0(舍去).
(3)若对于A中的每一个x值,都有f(x)=g(x),
即x2+1=4x+1,
∴x2=4x,
解得x=4或x=0,
∴满足题意的集合是{0],或{4}或{0,4}.
点评:本题主要考查了二次函数、一次函数的性质,集合相等,集合的表示方法.考查对知识的准确理解与掌握.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
若用秦九韶算法求多项式f(x)=4x5-x2+2当x=3时的值,则需要做乘法运算和加减法运算的次数分别为( )
| A、4,2 | B、5,3 |
| C、5,2 | D、6,2 |
2012年上海市居民的支出构成情况如下表所示:
用下列哪种统计图表示上面的数据最合适( )
| 食品 | 衣着 | 家庭设备用品及服务 | 医疗保健 | 交通和通讯 | 教育文化娱乐服务 | 居住 | 杂项商品和服务 |
| 39.4% | 5.9% | 6.2% | 7.0% | 10.7% | 15.9% | 11.4% | 3.5% |
| A、条形统计图 | B、茎叶图 |
| C、扇形统计图 | D、折线统计图 |
如图是一个正三角形场地,如果在每边上放2盆花共需要3盆花;如果在每边上放3盆花共需要6盆花,如果在每边上放n(n>1)盆花,那么共需要花( )盆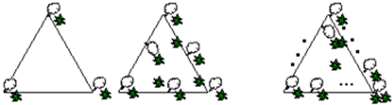

| A、3n | B、3n-1 |
| C、3n-2 | D、3n-3 |
已知△ABC中,内角A,B,C所对边长分别为a,b,c,若A=
,b=2acosB,c=1,则△ABC的面积等于( )
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知椭圆C1:
如图,已知椭圆C1: