Question

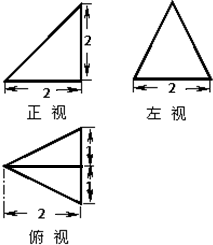已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），那么可得这个几何体的体积是（　　）

• A、

  1

  3

  cm³
• B、

  2

  3

  cm³
• C、

  4

  3

  cm³
• D、

  8

  3

  cm³

Answer 1

考点：由三视图求面积、体积

专题：计算题

分析：由三视图判断几何体为三棱锥，求出三棱锥的高与底面面积，代入棱锥的体积公式计算．．

解答： 解：由三视图判断几何体为三棱锥，且三棱锥的高为2，底面三角形底边长和高都为2．
∴棱锥的体积V=

1

3

×

1

2

×2×2×2=

4

3

（cm）．
故选C．

点评：本题考查由三视图求几何体的体积，解题的关键是判断几何体的形状及相关数据所对应的几何量．