Question

如图：有一块半径为2的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底是圆的直径，上底CD的端点在圆周上．梯形的周长令为y，腰长为x
（Ⅰ）求周长y关于腰长x的函数关系式，并求其定义域；
（Ⅱ）当梯形周长最大时，求此时梯形的面积S．

Answer 1

考点：函数解析式的求解及常用方法,函数的最值及其几何意义

专题：函数的性质及应用

分析：（ I）画出图形，结合图形，求出周长y关于腰长x的函数解析式，再求出函数的定义域即可；
（Ⅱ）求出函数y的最大值，并求出此时对应的梯形的面积S．

解答： 解：（ I）如图所示，作DE⊥AB于E，连接BD，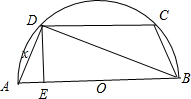
因为AB为直径，所以∠ADB=90°；
在Rt△ADB与Rt△AED中，∠ADB=90°=∠AED，∠BAD=∠DAE，
所以Rt△ADB∽Rt△AED；
所以

AD

AB

=

AE

AD

，即AE=

AD2

AB

；
又AD=x，AB=4，所以AE=

x2

4

；
所以CD=AB-2AE=4-2×

x2

4

=4-

x2

2

，
于是y=AB+BC+CD+AD=4+x+4-

x2

2

+x=-

1

2

x²+2x+8，
由于AD＞0，AE＞0，CD＞0，所以x＞0，

x2

4

＞0，4-

x2

2

＞0，
解得0＜x＜2

2

；
故所求的函数为y=-

1

2

x²+2x+8（0＜x＜2

2

）；
（Ⅱ）因为y=-

1

2

x²+2x+8=-

1

2

（x-2）²+10，
又0＜x＜2

2

，所以，当x=2时，y有最大值10，
此时，梯形的腰长AD=x=2，下底长AB=4，所以AE=

x2

4

=1；
所以上底长CD=AB-2AE=4-2×1=2，高DE=

3

；
∴梯形的面积为S=

1

2

（AB+CD）•DE=

1

2

×（4+2）×

3

=3

3

．

点评：本题考查了函数模型的应用问题，也考查了求函数最值的问题，是综合性题目．