题目内容
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
=0.85x-85.71,则下列结论中不正确的是( )
 |
| y |
| A、若该大学某女生身高为170cm,则可断定其体重必为58.79kg | ||||
B、回归直线过样本点的中心(
| ||||
| C、若该大学某女生身高增加1cm,则其体重约增加0.85kg | ||||
| D、y与x具有正的线性相关关系 |
考点:线性回归方程
专题:计算题,概率与统计
分析:根据回归方程为y=0.85x-85.71,0.85>0,可知B,C,D均正确,对于A回归方程只能进行预测,但不可断定.
解答:
解:对于A,x=170cm时,y=0.85×170-85.71=58.79,但这是预测值,不可断定其体重为58.79kg,故不正确
对于B,回归直线过样本点的中心(
,
),故正确;
对于C,∵回归方程为y=0.85x-85.71,∴该大学某女生身高增加1cm,则其体重约增加0.85kg,故正确;
对于A,0.85>0,所以y与x具有正的线性相关关系,故正确;
故选:A.
对于B,回归直线过样本点的中心(
. |
| x |
. |
| y |
对于C,∵回归方程为y=0.85x-85.71,∴该大学某女生身高增加1cm,则其体重约增加0.85kg,故正确;
对于A,0.85>0,所以y与x具有正的线性相关关系,故正确;
故选:A.
点评:本题考查线性回归方程,考查学生对线性回归方程的理解,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知复数(2-i)z=1+2i,
是z的共轭复数,则
等于( )
. |
| z |
. |
| z |
| A、1 | B、i | C、-1 | D、-i |
下列命题中,假命题为( )
A、若
| ||||||||||||
B、若
| ||||||||||||
C、若k∈R,k
| ||||||||||||
D、若
|
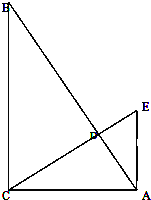 △ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.
△ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.