题目内容
已知函数f(x)=lnx-
+a(其中a∈R,无理数e=2.71828…).当x=e时,函数f(x)有极大值
.
(1)求实数a的值;
(2)求函数f(x)的单调区间;
(3)任取x1,x2∈[e,e2],证明:|f(x1)-f(x2)|<3.
| x2 |
| 2e2 |
| 1 |
| 2 |
(1)求实数a的值;
(2)求函数f(x)的单调区间;
(3)任取x1,x2∈[e,e2],证明:|f(x1)-f(x2)|<3.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)将x=e代入函数的表达式求出a的值即可;(2)先求出函数的导数,从而求出函数的单调区间;(3)问题转化为证明|f(x)max-f(x)min|<3即可.
解答:
解:(1)由题知f(e)=lne-
+a=
,解得a=0;
(2)由题可知函数f(x)的定义域为(0,+∞),
又f′(x)=
-
=
=
,
由
>0得0<x<e;
<0得x>e;
故函数f(x)单调增区间为(0,e),单调减区间为(e,+∞);
(3)因为f(x)=lnx-
,由(1)知函数f(x)的单调减区间为(e,+∞),
故f(x)在[e,e2]上单调递减,
∴f(x)max=f(e)=lne-
=1-
=
;
f(x)min=f(e2)=lne2-
=2-
,
∴f(x)max-f(x)min=
-(2-
)=
,
∴|f(x)max-f(x)min|=
<3①,
依题意任取x1,x2∈[e,e2],欲证明|f(x1)-f(x2)|<3,
只需要证明∴|f(x)max-f(x)min|<3即可,
由①可知此式成立,所以原命题得证.
| e2 |
| 2e2 |
| 1 |
| 2 |
(2)由题可知函数f(x)的定义域为(0,+∞),
又f′(x)=
| 1 |
| x |
| x |
| e2 |
| e2-x2 |
| e2x |
| (e+x)(e-x) |
| e2x |
由
| (e+x)(e-x) |
| e2x |
| (e+x)(e-x) |
| e2x |
故函数f(x)单调增区间为(0,e),单调减区间为(e,+∞);
(3)因为f(x)=lnx-
| x2 |
| 2e2 |
故f(x)在[e,e2]上单调递减,
∴f(x)max=f(e)=lne-
| e2 |
| 2e2 |
| 1 |
| 2 |
| 1 |
| 2 |
f(x)min=f(e2)=lne2-
| e4 |
| 2e2 |
| e2 |
| 2 |
∴f(x)max-f(x)min=
| 1 |
| 2 |
| e2 |
| 2 |
| e2-3 |
| 2 |
∴|f(x)max-f(x)min|=
| e2-3 |
| 2 |
依题意任取x1,x2∈[e,e2],欲证明|f(x1)-f(x2)|<3,
只需要证明∴|f(x)max-f(x)min|<3即可,
由①可知此式成立,所以原命题得证.
点评:本题考查了导数的应用,考查了函数的单调性,绝对值不等式的证明,本题属于中档题.

练习册系列答案
相关题目
已知复数(2-i)z=1+2i,
是z的共轭复数,则
等于( )
. |
| z |
. |
| z |
| A、1 | B、i | C、-1 | D、-i |
某几何体的三视图如图所示,它的体积为( )


| A、81π | B、57π |
| C、45π | D、12π |
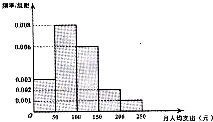 如图为某市地铁乘客的月人均乘坐地铁费用支出的频率分布直方图,若按直方图中的五段分层,并使用分层抽样方法从该市地铁乘客中抽取40人参加听证会,则所抽取的40人中月人均乘坐地铁费用支出在[100,150)的人数为( )
如图为某市地铁乘客的月人均乘坐地铁费用支出的频率分布直方图,若按直方图中的五段分层,并使用分层抽样方法从该市地铁乘客中抽取40人参加听证会,则所抽取的40人中月人均乘坐地铁费用支出在[100,150)的人数为( )| A、4 | B、8 | C、12 | D、16 |
下列命题中,假命题为( )
A、若
| ||||||||||||
B、若
| ||||||||||||
C、若k∈R,k
| ||||||||||||
D、若
|
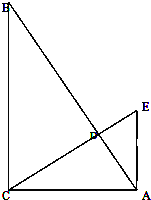 △ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.
△ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.