题目内容

已知整数数列a0，a1，a2，…，a2014中，满足关系式a0=0，|a1|=|a0+1|，|a2|=|a1+1|，…，|a2014|=|a2013+1|，则|a1+a2+a3+…+a2014|的最小值为
 
．
考点：数列的求和
专题：等差数列与等比数列
分析：由a0=0，|a1|=|a0+1|，可得a1=±1；同理可得：a2，a3，a4，…，可得|a1+a2|的最小值为1；|a1+a2+a3+a4|的最小值为2；依此类推可得：|a1+a2+a3+…+a2014|的最小值．
解答： 解：由a0=0，|a1|=|a0+1|，可得a1=±1；同理可得：a2=±2，或0；a3=±3，±1；a4=±4，±2，0；…；
可得|a1+a2|的最小值为1；|a1+a2+a3+a4|的最小值为2；
依此类推可得：|a1+a2+a3+…+a2014|的最小值为1007．
故答案为：1007．
点评：本题考查了推式的应用、绝对值的意义、类比归纳推理，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
已知平面α，β，直线m，n，给出下列命题：
①若m∥α，n∥β，m⊥n，则α⊥β，②若α∥β，m∥α，n∥β，则m||n，③若m⊥α，n⊥β，m⊥n，则α⊥β，④若α⊥β，m⊥α，n⊥β，则m⊥n．
其中是真命题的是
 
．（填写所有真命题的序号）．
设a=log3
2
3
，b=log5
2
5
，c=log7
2
7
，则（　　）
A、c＞b＞a
B、b＞c＞a
C、a＞c＞b
D、a＞b＞c
已知抛物线C：x2=2y的焦点为F．
（Ⅰ）设抛物线上任一点P（m，n）．求证：以P为切点与抛物线相切的方程是mx=y+n；
（Ⅱ）若过动点M（x0，0）（x0≠0）的直线l与抛物线C相切，试判断直线MF与直线l的位置关系，并予以证明．
如图，将∠B=
π
3
，边长为1的菱形ABCD沿对角线AC折成大小等于θ的二面角B-AC-D，若θ∈[
π
3
，
2π
3
]，M、N分别为AC、BD的中点，则下面的四种说法：
①AC⊥MN；
②DM与平面ABC所成的角是θ；
③线段MN的最大值是
3
4
，最小值是
3
4
；
④当θ=
π
2
时，BC与AD所成的角等于
π
2
．
其中正确的说法有
 
（填上所有正确说法的序号）．
在直角坐标平面内，过点P（0，3）的直线与圆心为C的圆x2+y2-2x-3=0相交于A，B两点，则△ABC面积的最大值是（　　）
A、2
B、4
C、
3
D、2
3
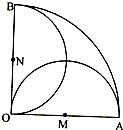如图，在圆心角为直角的扇形OAB区域中，M、N分别为OA、OB的中点，在M、N两点处各有一个通信基站，其信号的覆盖范围分别为以OA、OB为直径的圆，在扇形OAB内随机取一点，则此点无信号的概率是（　　）
A、1-
2
π
B、
1
2
-
1
π
C、
1
2
+
1
π
D、
1
π
已知f（x）=cosx（cosx-3）+sinx（sinx-3）．
（1）若x∈[2π，3π]，求f（x）的单调递减区间；
（2）若x∈（
π
2
，
3π
4
）且f（x）=-1，求tan2x的值．
已知函数y=ax2+bx+c的图象关于x=-1对称，最大值为2，在y轴上的截距为1．
（1）求a，b，c的值；
（2）如果f（x）＞2，求对应x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网