题目内容
11.若空间中四条两两不同的直线l1,l2,l3,l4,满足l1∥l2,l3⊥l1,l4⊥l2,则下列结论一定正确的是( )| A. | l3⊥l4 | B. | l3∥l4 | ||
| C. | l3,l4既不平行也不垂直 | D. | l3,l4的位置关系不确定 |
分析 垂直于同一直线的两直线相交、平行或异面.
解答 解:∵空间中四条两两不同的直线l1,l2,l3,l4,
满足l1∥l2,l3⊥l1,l4⊥l2,
∴l3⊥l2,
又∵l4⊥l2,∴l4与l3的位置关系不确定,
故A、B、C错误.
故选:D.
点评 本题考查两直线位置关系的判断,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.过点(2,3)和点(6,5)的直线的斜率为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
20.椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为4,A、B两点的坐标分别为(x1,y1)和(x2,y2),则|y2-y1|的值为( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{5}{3}$ |
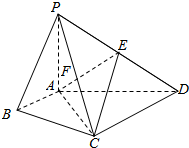 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.