题目内容
1.已知f′(x)=3x2-6x,且f(0)=4,解不等式f(x)>0.分析 根据导数和函数的关系,求出f(x),再解不等式即可.
解答 解:∵f′(x)=3x2-6x,
∴f(x)=x3-3x2+c,
∵f(0)=4,
∴c=4,
∴f(x)=x3-3x2+4=(x+1)(x-2)2,
∴(x+1)(x-2)2>0,
∴x>-1且x≠2,
故不等式f(x)>0的解集为(-1,2)∪(2,+∞).
点评 本题考查了函数和导数的关系,以及不等式的解法,属于基础题.

练习册系列答案
相关题目
11.已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示,则该正三棱锥侧视图的面积是( )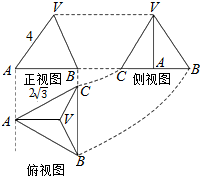

| A. | $\sqrt{39}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
16.某三棱锥的三视图如图所示,该三棱锥的表面积是( )
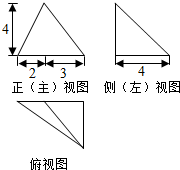

| A. | 56+12$\sqrt{5}$ | B. | 60+12$\sqrt{5}$ | C. | 30+6$\sqrt{5}$ | D. | 28+6$\sqrt{5}$ |
13.直线$y=x+\frac{1}{2}$与曲线x2-y|y|=1的交点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.若空间中四条两两不同的直线l1,l2,l3,l4,满足l1∥l2,l3⊥l1,l4⊥l2,则下列结论一定正确的是( )
| A. | l3⊥l4 | B. | l3∥l4 | ||
| C. | l3,l4既不平行也不垂直 | D. | l3,l4的位置关系不确定 |
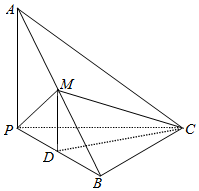 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.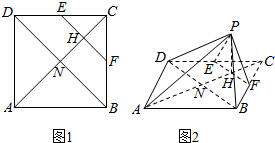 如图1,正方形ABCD的边长为$2\sqrt{2}$,E、F分别是DC和BC的中点,H是正方形的对角线AC与EF的交点,N是正方形两对角线的交点,现沿EF将△CEF折起到△PEF的位置,使得PH⊥AH,连结PA,PB,PD(如图2).
如图1,正方形ABCD的边长为$2\sqrt{2}$,E、F分别是DC和BC的中点,H是正方形的对角线AC与EF的交点,N是正方形两对角线的交点,现沿EF将△CEF折起到△PEF的位置,使得PH⊥AH,连结PA,PB,PD(如图2).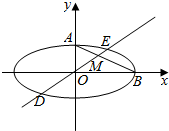 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.