题目内容
16.已知函数f(x)=x2-2cosx,对于$[{-\frac{π}{2},\frac{π}{2}}]$上的任意x1,x2,有如下条件:①x1>x2; ②$x_1^2>x_2^2$; ③|x1|>x2; ④x1>|x2|,其中能使$f({x_1})>f({x_2^{\;}})$恒成立的条件个数共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用导数可以判定其单调性,再判断出奇偶性,即可判断出结论.
解答 解:∵f(x)=x2-2cosx,∴f′(x)=2x+2sinx,
∴当x=0时,f′(0)=0;当x∈[-$\frac{π}{2}$,0)时,f′(x)<0,函数f(x)在此区间上单调递减;
当x∈(0,$\frac{π}{2}$]时,f′(x)>0,函数f(x)在此区间上单调递增.
∴函数f(x)在x=0时取得最小值,f(0)=0-1=-1.
∵x∈[-$\frac{π}{2}$,$\frac{π}{2}$],都有f(-x)=f(x),∴f(x)是偶函数.
根据以上结论可得:
①当x1>x2时,则f(x1)>f(x2)不成立;
②当x12>x22时,得|x1|>|x2|,则f(|x1|)>f(|x2|),f(x1)>f(x2)恒成立;
③当|x1|>x2时,由函数f(x)=x2-2cosx是偶函数,知f(x1)=f(|x1|)>f(x2)不恒成立;
④x1>|x2|时,则f(x1)>f(|x2|)=f(x2)恒成立.
综上可知:能使f(x1)>f(x2)恒成立的有②④.
故选:B.
点评 本题考查命题真假的判断,是中档题,熟练掌握利用导数研究函数的单调性、判定函数的奇偶性等是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
11.若空间中四条两两不同的直线l1,l2,l3,l4,满足l1∥l2,l3⊥l1,l4⊥l2,则下列结论一定正确的是( )
| A. | l3⊥l4 | B. | l3∥l4 | ||
| C. | l3,l4既不平行也不垂直 | D. | l3,l4的位置关系不确定 |
8.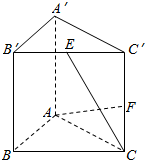 在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )
在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )
 在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )
在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
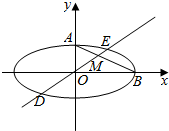 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.