题目内容
1．曲线$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$与曲线$\frac{x^2}{{{a^2}-m}}+\frac{y^2}{{{b^2}-m}}=1$有相同的（ ）| A． | 长轴长 | B． | 短轴长 | C． | 焦距 | D． | 离心率 |
分析 由题意，（a2-m）-（b2-m）=a2-b2，即可得出结论．
解答 解：由题意，（a2-m）-（b2-m）=a2-b2，
∴曲线$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$与曲线$\frac{x^2}{{{a^2}-m}}+\frac{y^2}{{{b^2}-m}}=1$有相同的焦距，
故选：C．
点评 本题考查椭圆的性质，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
11．若空间中四条两两不同的直线l1，l2，l3，l4，满足l1∥l2，l3⊥l1，l4⊥l2，则下列结论一定正确的是（ ）
| A． | l3⊥l4 | B． | l3∥l4 | ||
| C． | l3，l4既不平行也不垂直 | D． | l3，l4的位置关系不确定 |
12．
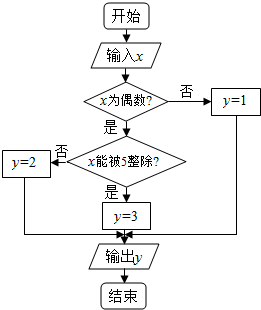某算法的程序框图如图所示，其中输入的变量J在1，2，3，…，30这30个整数中等可能随机产生．
（1）分别求出（按程序框图正确编程运行时）输出y的值为i的概率Pi（i=1，2，3）；
（2）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录
了输出y的值为i（i=1，2，3）的频数，下面是甲、乙所作频数统计表的部分数据：
甲的频数统计表（部分）
乙的频数统计表（部分）
当n=2000时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i（i=1，2，3）的频率（用分数表示），并判断甲、乙中谁所编写的程序符合算法要求的可能性较大．
某算法的程序框图如图所示，其中输入的变量J在1，2，3，…，30这30个整数中等可能随机产生．（1）分别求出（按程序框图正确编程运行时）输出y的值为i的概率Pi（i=1，2，3）；
（2）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录
了输出y的值为i（i=1，2，3）的频数，下面是甲、乙所作频数统计表的部分数据：
甲的频数统计表（部分）
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 16 | 11 | 3 |
| … | … | … | … |
| 2000 | 967 | 783 | 250 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 13 | 13 | 4 |
| … | … | … | … |
| 2000 | 998 | 803 | 199 |
10．已知椭圆$\frac{x^2}{9}+\frac{y^2}{n^2}=1$与双曲线$\frac{x^2}{4}-\frac{y^2}{m^2}=1$有相同的焦点，则动点P（n，m）的轨迹是（ ）
| A． | 椭圆的一部分 | B． | 双曲线的一部分 | C． | 抛物线的一部分 | D． | 圆的一部分 |