题目内容
2.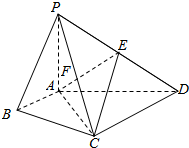 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=4.(1)求证:CE∥平面PAB;
(2)若F为PC的中点,求AF与平面AEC所成角的正弦值.
分析 (1)取AD得中点M,连接EM,CM.则EM∥PA,由∠CAD=60°,CM=AM,得MC∥AB.由此能证明CE∥平面PAB.
(2)以C为原点,CA为x轴,CD为y轴,过C作平面ABCD的垂线为z轴建立空间直角坐标系,利用向量法能求出AF与平面AEC所成角的正弦值.
解答 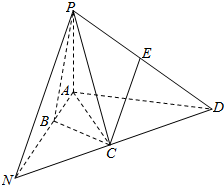 证明:(1)取AD得中点M,连接EM,CM.则EM∥PA,
证明:(1)取AD得中点M,连接EM,CM.则EM∥PA,
∵EM?平面PAB,PA?平面PAB,
∴EM∥平面PAB,
在Rt△ACD中,∠CAD=60°,CM=AM,∴∠ACM=60°,
而∠BAC=60°,∴MC∥AB.
∵MC?平面PAB,AB?平面PAB,
∴MC∥平面PAB,
又∵EM∩MC=M,
∴平面EMC∥平面PAB,
∵EC?平面EMC,∴CE∥平面PAB.
解:以C为原点,CA为x轴,CD为y轴,过C作平面ABCD的垂线为z轴,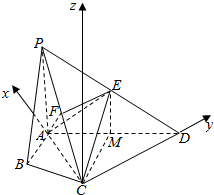
建立空间直角坐标系,
∵∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,
PA=2AB=4,F为PC的中点,
∴A(4,0,0),C(0,0,0),P(4,0,4),F(2,0,2),
D(0,4$\sqrt{3}$,0),E(2,2$\sqrt{3}$,2),
$\overrightarrow{AF}$=(-2,0,2),$\overrightarrow{CA}$=(4,0,0),$\overrightarrow{CE}$=(2,2$\sqrt{3}$,2),
设平面AEC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CA}=4x=0}\\{\overrightarrow{n}•\overrightarrow{CE}=2x+2\sqrt{3}y+2z=0}\end{array}\right.$,取y=$\sqrt{3}$,得$\overrightarrow{n}$=(0,$\sqrt{3}$,-3),
设AF与平面AEC所成角为θ,
则sinθ=$\frac{|\overrightarrow{AF}•\overrightarrow{n}|}{|\overrightarrow{AF}|•|\overrightarrow{n}|}$=$\frac{|-6|}{\sqrt{8}•\sqrt{12}}$=$\frac{\sqrt{6}}{4}$.
∴AF与平面AEC所成角的正弦值为$\frac{\sqrt{6}}{4}$.
点评 本题考查线面平行的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | l3⊥l4 | B. | l3∥l4 | ||
| C. | l3,l4既不平行也不垂直 | D. | l3,l4的位置关系不确定 |
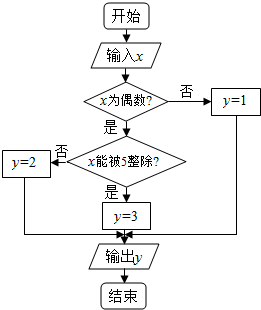 某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.
某算法的程序框图如图所示,其中输入的变量J在1,2,3,…,30这30个整数中等可能随机产生.(1)分别求出(按程序框图正确编程运行时)输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录
了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据:
甲的频数统计表(部分)
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 16 | 11 | 3 |
| … | … | … | … |
| 2000 | 967 | 783 | 250 |
| 运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
| 30 | 13 | 13 | 4 |
| … | … | … | … |
| 2000 | 998 | 803 | 199 |
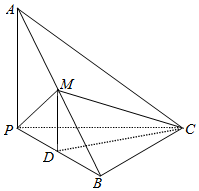 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.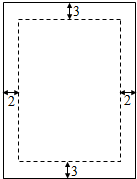 如图,有一矩形相框,放置照片区域的上、下方要各留3cm空白,左、右两侧要各留2cm的空白.
如图,有一矩形相框,放置照片区域的上、下方要各留3cm空白,左、右两侧要各留2cm的空白.