题目内容
双曲线C: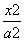 -
-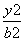 =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y= x,坐标原点到直线AB的距离为
x,坐标原点到直线AB的距离为 ,其中A(a,0),
,其中A(a,0), B(0,-b).
B(0,-b).
(1)求双曲线的方程;
(2)若B1是双曲线虚轴在y轴正半轴上的端点,过点B作直线交双曲线于点M,N,求当 时,直线MN的方程.
时,直线MN的方程.
解析:(1)设直线AB的方程为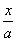 -
-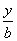 =1,由已知条件得
=1,由已知条件得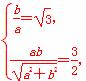 解得a=
解得a= ,b=3.
,b=3.
∴双曲线方程为 -
- =1.
=1.
(2)由(1)知B(0,-3),B1(0,3).设M(x1,y1),N(x2,y2),直线l:y=kx-3.
由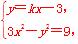 消去y,整理得(3-k2)·x2+6kx-18=0,
消去y,整理得(3-k2)·x2+6kx-18=0,
∴x1+x2=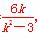 ,y1+y2=k(x1+x2)-6=
,y1+y2=k(x1+x2)-6=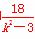 ,
,
x1x2=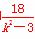 ,y1y2=k2x1x2-3k(x1+x2)+9=9.
,y1y2=k2x1x2-3k(x1+x2)+9=9.
∵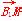 =(x1,y1-3),
=(x1,y1-3),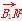 =(x2,y2-3),
=(x2,y2-3),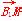 ·
·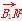 =0,
=0,
∴x1x2+y1y2-3(y1+y2)+9=0,
即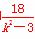 +9-
+9-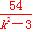 +9=0,解得k2=5,∴k=±
+9=0,解得k2=5,∴k=±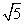 ,
,
代入y=kx-3中,得y=±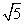 x-3为所求方程.
x-3为所求方程.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 A的中点B在抛物线上,则B到该抛物线准线的距离为________.
A的中点B在抛物线上,则B到该抛物线准线的距离为________. -
- =1的离心率为
=1的离心率为 , 则m=__________.
, 则m=__________. +
+ 的最小值是________.
的最小值是________.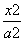 -
-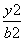 =1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )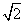 B.
B.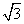 C.
C. D.
D.
 =1表示椭圆的( )
=1表示椭圆的( )