题目内容
1.在数列{an}和等比数列{bn}中,a1=0,a4=3,bn=2${\;}^{{a}_{n}+1}$(n∈N*).(Ⅰ)求数列{an}及{bn}的通项公式;
(Ⅱ)若cn=an•bn,求数列{cn}的前n项和Sn.
分析 (I)利用等比数列的通项公式即可得出.
(II)依题意cn=an•bn=(n-1)•2n.利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(Ⅰ)依题意b1=2,b4=24=16,
设数列{bn}的公比为q,由b4=${b}_{1}{q}^{3}$=2q3=16,得q3=8,解得q=2,
故bn=2×2n-1=2n,
又由${2}^{{a}_{n}+1}$=2n,得an=n-1.
(Ⅱ)依题意cn=an•bn=(n-1)•2n.
∴Sn=0+22+2×23+3×24+…+(n-1)•2n,①
则2Sn=0+23+2×24+…+(n-2)•2n+(n-1)•2n+1 ②
①-②得-Sn=22+23+…+2n-(n-1)•2n+1=$\frac{4({2}^{n-1}-1)}{2-1}$-(n-1)•2n+1=(2-n)•2n+1-4,
∴Sn=4+(n-2)•2n+1.
点评 本小题主要考查“错位相减法”、等比数列的通项公式与前n项和公式等基础知识,考查运算求解能力,考查函数与方程思想等,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
12.己知全集U=R,函数y=$\frac{1}{\sqrt{x+2}}$的定义域为集合A,函数y=log3(x+1)的定义域为B,则集合A∩(∁UB)=( )
| A. | (2,-1) | B. | (-2,-1] | C. | (-∞,-2) | D. | [-1,+∞) |
6.设函数f(x)=$\left\{\begin{array}{l}{4+x,x≤0}\\{{x}^{2},x>0}\end{array}\right.$,若f[f(a)]>f[f(a)+1],则实数a的取值范围为( )
| A. | (-1,0] | B. | [-1,0] | C. | (-5,-4] | D. | [-5,-4] |
13.一个空间几何体的三视图如图所示,则该几何体的外接球的表面积为( )
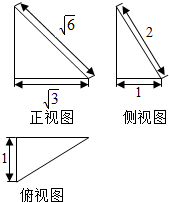

| A. | 5? | B. | 6? | C. | 2$\sqrt{7}$π | D. | 7π? |