题目内容

13．一个空间几何体的三视图如图所示，则该几何体的外接球的表面积为（　　）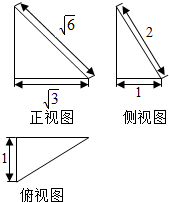
A．5?B．6?C．2$\sqrt{7}$πD．7π?

分析 由已知的三视图可得：该几何体是一个三棱锥，且从同一点出发的三条棱两两垂直，其长度分别为1，$\sqrt{3}$，$\sqrt{3}$，求出其外接球的半径，代入表面积公式，可得答案．

解答 解：该几何体是一个三棱锥，且从同一点出发的三条棱两两垂直，其长度分别为1，$\sqrt{3}$，$\sqrt{3}$，故该几何体的外接球的直径为$\sqrt{1+3+3}$=$\sqrt{7}$，∴该球的表面积为S=4πR2=7π．
故选：D．

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案
相关题目
3．若a2+1=2b2，a、b∈R，求函数y=|a-2b|的最小值．
4．给出以下四个命题：
①正态曲线当μ一定时曲线形状由σ确定，σ越小曲线越“瘦高”表示总体分布越集中；
②过点（-1，2）且在x轴和y轴上的截距相等的直线方程是x+y-1=0；
③函数f（x）=2x+2x-3在定义域内有且只有一个零点；
④回归方程拟合效果可用R2=1-$\frac{\sum_{i=1}^{n}（{y}_{i}-\stackrel{∧}{{y}_{i}}）^{2}}{\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}$刻画，R2越接近1表示回归效果越差；
其中正确命题的序号为①③．（把你认为正确的命题序号都填上）
1．在数列{an}和等比数列{bn}中，a1=0，a4=3，bn=2${\;}^{{a}_{n}+1}$（n∈N*）．
（Ⅰ）求数列{an}及{bn}的通项公式；
（Ⅱ）若cn=an•bn，求数列{cn}的前n项和Sn．
8．（2+x+x2）（1-$\frac{1}{x}$）3的展开式中常数项为（　　）
A．-2B．5C．4D．2
18．己知直线l1：mx-y+2=0（m∈R），直线l2：x+my-2=0，点P是两直线的交点．
（1）判断两直线l1、l2的位置关系，并求点P的轨迹C的方程；
（2）已知M（1，1），设Q是直线x+y+2=0上的动点，QA．QB是轨迹C的两条切线，A，B为切点，求四边形QAMB的面积的最小值．
5．已知函数f（x）=x2+2ax-3．
（1）求实数a的取值范围，使得y=f（x）在区间[-4，6]上是单调函数；
（2）当x∈[-4，6]时，求f（x）的最小值g（a）；
（3）画出分段函数g（x）图象，求g（x）的最大值．
2．若实数k∈[-2，3]，则函数f（x）=kx+1在[-1，1]上恒大于0的概率是（　　）
A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$
3．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\sqrt{2}$，|$\overrightarrow{b}$|=1，若|$\overrightarrow{a}$-$\overrightarrow{b}$|=2，试求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网