题目内容
14.利用计算机随机模拟方法计算y=4x2与y=4所围成的区域Ω的面积时,可以先运行以下算法步骤:第一步:利用计算机产生两个在[0,1]区间内的均匀随机数a,b;
第二步:对随机数a,b实施变换:$\left\{\begin{array}{l}{{a}_{1}=2a-1}\\{{b}_{1}=4b}\end{array}\right.$,得到点A(a1,b1);
第三步:判断点A(a1,b1)的坐标是否满足b1<4${a}_{1}^{2}$;
第四步:累计所产生的点A的个数m,及满足b1<4${a}_{1}^{2}$的点A的个数n;
第五步:判断m是否小于M(一个设定的数).若是,则回到第一步,否则,输出n并终止算法.
若设定的M=150,且输出的n=51,则据此用随机模拟方法可以估计出区域Ω的面积为$\frac{132}{25}$.
分析 由第三步可知,n表示y=4x2下方的点A的个数,其概率为$\frac{n}{M}$=$\frac{51}{150}$,故点落在y=4x2上方的概率为1-$\frac{n}{M}$=1-$\frac{51}{150}$=$\frac{33}{50}$;先由计算器做模拟试验结果试验估计,得出点落在阴影部分的点的概率,再转化为几何概型的面积类型求解区域Ω的面积S.
解答 解:由第三步可知,n表示y=4x2下方的点A的个数,其概率为$\frac{n}{M}$=$\frac{51}{150}$,故点落在y=4x2上方的概率为1-$\frac{n}{M}$=1-$\frac{51}{150}$=$\frac{33}{50}$;
矩形的面积为4×2=8,
设区域Ω的面积为S,则有$\frac{S}{8}$=$\frac{33}{50}$,
∴S=$\frac{33}{50}$×8=$\frac{132}{25}$.
故答案为:$\frac{132}{25}$.
点评 本题考查模拟方法估计概率以及几何概型中面积类型,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
9.若函数g(x)=sin4x+$\sqrt{3}$cos4x-1,则下面对函数y=g(x)的叙述正确的是( )
| A. | 曲线y=g(x)的一个对称中心为点(-$\frac{π}{12}$,0) | |
| B. | 曲线y=g(x)的一个对称轴为直线x=$\frac{kπ}{4}$+$\frac{π}{16}$(k∈Z) | |
| C. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内单调递减 | |
| D. | 函数y=g(x)在区间[$\frac{2π}{3}$,$\frac{3π}{4}$]内不单调 |
3.函数f(x)=sin4x+acos4x图象的一条对称轴方程是直线x=$\frac{π}{6}$,则a=( )
| A. | 1 | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
6.△ABC的周长等于20,面积是$10\sqrt{3}$,A=60°,则角A的对边长为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
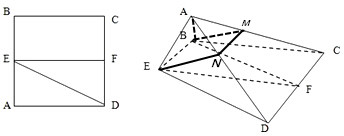 已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.
已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.