题目内容
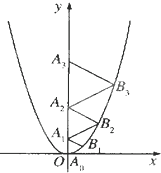 二次函数y=
二次函数y=| 1 |
| 3 |
| 1 |
| 3 |
考点:数列与函数的综合
专题:综合题,等差数列与等比数列
分析:先计算出△A0B1A1;△A1B2A2;△A2B3A2的边长,推理出各边长组成的数列各项之间的排列规律,即可得出结论.
解答:
解:作B1A⊥y轴于A,B2B⊥y轴于B,B3C⊥y轴于C.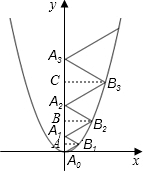
设等边△A0B1A1、△A1B2A2、△A2B3A3中,AA1=a,BA2=b,CA2=c.
①等边△A0B1A1中,A0A=a,
所以B1A=atan60°=
a,代入解析式得
×(
a)2=a,
解得a=0(舍去)或a=1,于是等边△A0B1A1的边长为1×2=2;
②等边△A2B1A1中,A1B=b,
所以BB2=btan60°=
b,B2点坐标为(
b,2+b)
代入解析式得
×(
b)2=2+b,
解得b=-1(舍去)或b=2,
于是等边△A2B1A1的边长为2×2=4;
于是n个等边三角形An-1BnAn(n≥1的整数)的边长是2n.
故答案为:2n.

设等边△A0B1A1、△A1B2A2、△A2B3A3中,AA1=a,BA2=b,CA2=c.
①等边△A0B1A1中,A0A=a,
所以B1A=atan60°=
| 3 |
| 1 |
| 3 |
| 3 |
解得a=0(舍去)或a=1,于是等边△A0B1A1的边长为1×2=2;
②等边△A2B1A1中,A1B=b,
所以BB2=btan60°=
| 3 |
| 3 |
代入解析式得
| 1 |
| 3 |
| 3 |
解得b=-1(舍去)或b=2,
于是等边△A2B1A1的边长为2×2=4;
于是n个等边三角形An-1BnAn(n≥1的整数)的边长是2n.
故答案为:2n.
点评:此题主要考查了二次函数和等边三角形的性质的综合应用,将其性质结合在一起,增加了题目的难度,是一道开放题,有利于培养同学们的探索发现意识.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
在一次抽奖活动中,有甲、乙等6人获得抽奖的机会,已知甲中奖的概率为0.6,乙中奖的概率为0.5,甲、乙是否中奖不受影响,则甲、乙都中奖的概率是( )
| A、0.6 | B、0.5 |
| C、0.3 | D、0.2 |
 如图所示,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,已知PA=6,AB=
如图所示,⊙O的割线PAB交⊙O于A、B两点,割线PCD经过圆心O,已知PA=6,AB=