题目内容
| ∫ | 2 1 |
考点:定积分
专题:导数的综合应用
分析:利用定积分的计算解答,求出被积函数的原函数,计算定积分.
解答:
解:
(1+x)dx═(x+
x2)|
=2+2-1-
=
;
故答案为:
.
| ∫ | 2 1 |
| 1 |
| 2 |
2 1 |
| 1 |
| 2 |
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查了定积分的运算,关键是熟记常用函数的导数,才能熟练求被积函数的原函数.

练习册系列答案
相关题目
给定条件p:|x+1|>2,条件q:
>1,则?p是?q的 ( )
| 1 |
| 3-x |
| A、既不充分也不必要条件 |
| B、必要而不充分条件 |
| C、充分而不必要条件 |
| D、充要条件 |
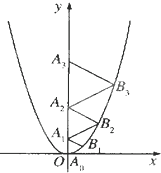 二次函数y=
二次函数y=