题目内容
12.已知函数f(x)=$\frac{{ln({2x})}}{x}$,关于x的不等式f2(x)+af(x)>0只有两个整数解,则实数a的取值范围为(-ln2,-$\frac{ln6}{3}$].分析 判断函数f(x)的单调性和取值情况,利用一元二次不等式的解法,结合数形结合进行求解即可.
解答 解:函数f(x)的定义域为(0,+∞),则f′(x)=$\frac{1-ln(2x)}{{x}^{2}}$.
当f′(x)>0得1-ln(2x)>0,即ln(2x)<1,即0<2x<e,即0<x<$\frac{e}{2}$,
由f′(x)<0得1-ln(2x)<0,得ln(2x)>1,即2x>e,即x>$\frac{e}{2}$,
即当x=$\frac{e}{2}$时,函数f(x)取得极大值,同时也是最大值f($\frac{e}{2}$)=$\frac{2}{e}$,
即当0<x<$\frac{e}{2}$时,f(x)<$\frac{2}{e}$有一个整数解1,
当x>$\frac{e}{2}$时,0<f(x)<$\frac{2}{e}$有无数个整数解,
①若a=0,则f2(x)+af(x)>0得f2(x)>0,此时有无数个整数解,不满足条件.
②若a>0,则由f2(x)+af(x)>0得f(x)>0或f(x)<-a,当f(x)>0时,
不等式由无数个整数解,不满足条件.
③当a<0时,由f2(x)+af(x)>0得f(x)>-a或f(x)<0,当f(x)<0时,没有整数解,
∵f(1)=ln2,f(2)=ln2,f(3)=$\frac{ln6}{3}$,
∴当f(x)≥ln2时,函数有两个整数点1,2,当f(x)≥$\frac{ln6}{3}$时,函数有3个整数点1,2,3
∴要使f(x)>-a有两个整数解,必有$\frac{ln6}{3}$≤-a<ln2,即-ln2<a≤-$\frac{1}{3}$ln6,
故答案为(-ln2,-$\frac{ln6}{3}$]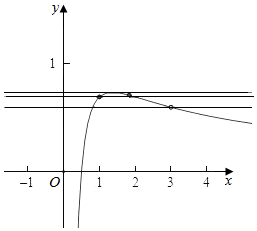
点评 本题主要考查不等式的求解,根据条件判断函数的取值范围,利用数形结合结合一元二次不等式的解法是解决本题的关键.综合性较强,属于难题.

| A. | -257 | B. | 13 | C. | 1855 | D. | -1855 |
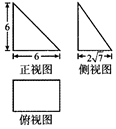 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )| A. | 100π cm2 | B. | $\frac{500π}{3}$ cm2 | C. | 400π cm2 | D. | $\frac{4000π}{3}$ cm2 |
 如图,在△ABC中,cos∠ABC=$\frac{1}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则△ABC的面积为2$\sqrt{2}$.
如图,在△ABC中,cos∠ABC=$\frac{1}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则△ABC的面积为2$\sqrt{2}$.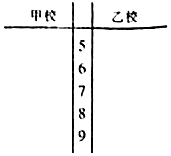 某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下: