题目内容
11.已知点P在椭圆C1:$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{4}$=1上,点Q在椭圆C2:$\frac{{y}^{2}}{9}$+x2=1上,O为坐标原点,记ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$,集合{(P,Q)|ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$},当ω取得最大值时,集合中符合条件的元素有几个( )| A. | 2个 | B. | 4个 | C. | 8个 | D. | 无数个 |
分析 由题意设P和Q的坐标,根据向量数量积的坐标运算及两角和的余弦定理,根据余弦函数的性质,即可判断集合中符合条件的元素个数.
解答 解:P(6cosα,2sinα),α∈[0,2π),Q(cosβ,3sinβ),α∈[0,2π),
$\overrightarrow{OP}$=(6cosα,2sinα),$\overrightarrow{OQ}$=(cosβ,3sinβ),
由ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$=6cosαcosβ+6sinαsinβ=6cos(α-β),-2π<α-β<2π,
∴α-β=2kπ,
∴k=0,则α=β,
∴当P和Q共线时,ω取得最大值,
故这样的点有无数个,
故选:D.
点评 本题考查椭圆的参数方程,向量数量积的坐标运算,两角和的余弦公式,余弦函数的性质,考查计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.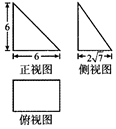 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )
 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )| A. | 100π cm2 | B. | $\frac{500π}{3}$ cm2 | C. | 400π cm2 | D. | $\frac{4000π}{3}$ cm2 |
19.已知集合A={x∈R|0<x≤5},B={x∈R|log2x<2},则(∁AB)∩Z=( )
| A. | {4} | B. | {5} | C. | [4,5] | D. | {4,5} |
11.函数y=(x+1)3当x=-1时( )
| A. | 有极大值 | B. | 有极小值 | ||
| C. | 既无极大值,也无极小值 | D. | 无法判断 |
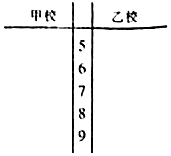 某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下: