Question

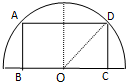在半径为4的半圆形铁皮内剪取一个内接矩形ABCD，如图（B，C两点在直径上，A，D两点在半圆周上），以边AB为母线，矩形ABCD为侧面围成一个圆柱，当圆柱侧面积最大时，该圆柱的体积为

 

．

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：计算题,空间位置关系与距离

分析：设AB=x，OB=y，则x²+y²=16，利用基本不等式求得x=y=2

2

时，圆柱侧面积最大，再求圆柱的体积．

解答： 解：设AB=x，OB=y，则x²+y²=16，
S_侧面积=2xy≤x²+y²=16，当且仅当x=y=2

2

时，圆柱侧面积最大，
设圆柱的底面半径为r，则2πr=4

2

，∴r=

2 2

π

，
∴V=π×（

2 2

π

）²×2

2

=

16 2

π

．
故答案为：

16 2

π

．

点评：本题考查圆柱的体积，考查学生的计算能力，考查基本不等式的运用，属于中档题．