题目内容

计算下列各式：
（1）
1
5
+2
-（
3
-1）0-
(2-5)2
；
（2）（2a 
2
3
b 
1
2
）（-6a 
1
2
b 
1
3
）÷（-3a 
1
6
b 
5
6
）
考点：根式与分数指数幂的互化及其化简运算
专题：计算题
分析：（1）分母有理化，化0指数幂为1，整理后得答案；
（2）先计算系数，然后利用同底数幂的乘除运算化简求值．
解答： 解：（1）
1
5
+2
-（
3
-1）0-
(2-5)2

=
5
-2
(
5
+2)(
5
-2)
-1-3
=
5
-2-1-3
=
5
-6；
（2）（2a 
2
3
b 
1
2
）（-6a 
1
2
b 
1
3
）÷（-3a 
1
6
b 
5
6
）
=4a
2
3
+
1
2
-
1
6
b
1
2
+
1
3
-
5
6

=4a
7
6
-
1
6
b0
=4a．
点评：本题考查了根式与分数指数幂的互化及其化简运算，是基础的计算题．
练习册系列答案
相关题目
设集合M={x|x-m＜0}，N={y|y=ax-1，a＞0且a≠1}，若M∩N=∅，则m的范围是（　　）
A、m≥-1B、m＞-1
C、m≤-1D、m＜-1
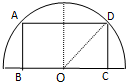在半径为4的半圆形铁皮内剪取一个内接矩形ABCD，如图（B，C两点在直径上，A，D两点在半圆周上），以边AB为母线，矩形ABCD为侧面围成一个圆柱，当圆柱侧面积最大时，该圆柱的体积为
 
．
已知曲线C：x2+y2-2x-4y+m=0．
（1）当m为何值时，曲线C表示圆；
（2）在（1）的条件下，若曲线C与直线3x+4y-6=0交于M、N两点，且|MN|=3
3
，求m的值；
（3）在（1）的条件下，设直线x-y-1=0与圆C交于A，B两点，是否存在实数m，使得以AB为直径的圆过原点，若存在，求出实数m的值；若不存在，请说明理由．
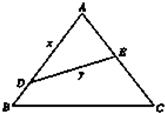如图，公园要把一块边长为2a的等边三角形ABC的边角地修成草坪，DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
（1）设AD=x（x≥a），DE=y，试用x表示函数y；
（2）如果DE是灌溉水管，希望它最短，D、E的位置应该在哪里？
已知α，β∈（
3
4
π，π），sin（α+β）=-
3
5
．
（Ⅰ）求sin2（α+β）的值；
（Ⅱ）若sin（β-
π
4
）=
3
10
10
，（i）求cos（α+
π
4
）的值（ii）求sin2α的值．
已知函数f（x）=
1-sin2x
cosx

（Ⅰ）若f（x）＞0，求x的取值范围；
（Ⅱ）设α是第四象限的角，且tanα=-
4
3
，求f（α）的值．
已知函数f（x）=3sin（
1
2
x-
π
4
）．x∈R．
（1）列表并画出函数f（x）在长度为一个周期的闭区间上的简图；
（2）将函数y=sinx的图象作怎样的变换可得到f（x）的图象？
已知sin（
π
4
-α）=-
4
5
，sin（
3π
4
+β）=
5
13
，且α∈（
π
4
，
3π
4
），β∈（0，
π
4
），求sin（α-β）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网