题目内容
若a＞0，b＞0，且函数f（x）=2x3-
ax2-bx+5在x=1处的切线的斜率为零，则ab的最大值等于（ ）
| 1 |
| 2 |
| A、2 | B、3 | C、6 | D、9 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用,不等式的解法及应用
分析：求出导数，由条件得到f′（1）=0，再由基本不等式的变形：ab≤（
）2即可得到最大值．
| a+b |
| 2 |
解答：
解：f′（x）=6x2-ax-b，
∵在x=1处的切线的斜率为零，
∴f′（1）=6-a-b=0
即a+b=6，
则ab≤（
）2=9．
当且仅当a=b=3时，取最大值9．
故选：D．
∵在x=1处的切线的斜率为零，
∴f′（1）=6-a-b=0
即a+b=6，
则ab≤（
| a+b |
| 2 |
当且仅当a=b=3时，取最大值9．
故选：D．
点评：本题考查了导数的几何意义，同时考查了基本不等式求最值．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
椭圆
+
=1上的一点M到一条准线的距离与它到对应于这条准线的焦点的距离之比为 （ ）
| x2 |
| 9 |
| y2 |
| 16 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合M={x|x-m＜0}，N={y|y=ax-1，a＞0且a≠1}，若M∩N=∅，则m的范围是（ ）
| A、m≥-1 | B、m＞-1 |
| C、m≤-1 | D、m＜-1 |
（a-2i）i=b-i，其中a、b∈R，i是虚数单位，则a2+b2=（ ）
| A、3 | B、5 | C、4 | D、2 |
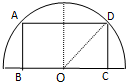在半径为4的半圆形铁皮内剪取一个内接矩形ABCD，如图（B，C两点在直径上，A，D两点在半圆周上），以边AB为母线，矩形ABCD为侧面围成一个圆柱，当圆柱侧面积最大时，该圆柱的体积为