题目内容
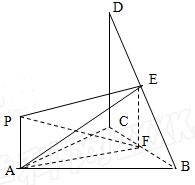
 如图,△BCD所在的平面垂直于正三角形ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点.
如图,△BCD所在的平面垂直于正三角形ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点.(1)证明:P、A、E、F四点共面;
(2)证明:AE⊥BC;
(3)求直线PF与平面BCD所成角的大小.
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)通过平面BCD⊥平面ABC,结合直线与平面平行的性质定理,推出EF∥PA,即可证明A,E,F四点共面.(2)连AF,EF,推出BC⊥平面AEF,利用直线与平面垂直的性质定理证明AE⊥BC.
(3)推出PA⊥平面ABC,证明AF⊥平面BCD,说明PF在平面BCD内射影为EF,然后说明∠PFE即为所求,求解即可.
(3)推出PA⊥平面ABC,证明AF⊥平面BCD,说明PF在平面BCD内射影为EF,然后说明∠PFE即为所求,求解即可.
解答:
 解:(1)证明:平面BCD⊥平面ABC,
解:(1)证明:平面BCD⊥平面ABC,
平面BCD∩平面ABC=BCCD⊥BC,CD?平面BCD,
CD⊥平面ABC∵PA⊥平面ABC∴PA∥CD,PA=
CD△BCD中,E、F分别为DB、CB的中点∴EF∥DC,EF=
CD∴EF∥PA,EF=PA
P,A,E,F四点共面-------------------------(4分)
(2)证明:连AF,EF,△ABC中,AC=BC,F为BC的中点,AF⊥BC,∠BCD=90°,DC∥EF,∴EF⊥BC,AF∩EF=F
BC⊥平面AEF,
AE?平面AEF∴AE⊥BC-------------------------------(8分)
(3)解:∴PA∥CD∵PA⊥平面ABC,
CD⊥平面ABC,AF?平面ABC,AF⊥CD,
∵AB=AC,BF=CF∴AF⊥BC,BC∩CD=C,
∴AF⊥平面BCD,
∵PE∥AF∴PE⊥平面BCD,
PF在平面BCD内射影为EF,
∴∠PFE即为所求.
可求∠PFE=60°,
直线PF与平面BCD所成角的大小为60°-----------------------(12分)
 解:(1)证明:平面BCD⊥平面ABC,
解:(1)证明:平面BCD⊥平面ABC,平面BCD∩平面ABC=BCCD⊥BC,CD?平面BCD,
CD⊥平面ABC∵PA⊥平面ABC∴PA∥CD,PA=
| 1 |
| 2 |
| 1 |
| 2 |
P,A,E,F四点共面-------------------------(4分)
(2)证明:连AF,EF,△ABC中,AC=BC,F为BC的中点,AF⊥BC,∠BCD=90°,DC∥EF,∴EF⊥BC,AF∩EF=F
BC⊥平面AEF,
AE?平面AEF∴AE⊥BC-------------------------------(8分)
(3)解:∴PA∥CD∵PA⊥平面ABC,
CD⊥平面ABC,AF?平面ABC,AF⊥CD,
∵AB=AC,BF=CF∴AF⊥BC,BC∩CD=C,
∴AF⊥平面BCD,
∵PE∥AF∴PE⊥平面BCD,
PF在平面BCD内射影为EF,
∴∠PFE即为所求.
可求∠PFE=60°,
直线PF与平面BCD所成角的大小为60°-----------------------(12分)
点评:本题考查直线与平面垂直的性质,直线与平面所成角的求法,平面的基本性质的应用,考查空间想象能力以及转化思想的应用.

练习册系列答案
相关题目
设a,b∈R,则“a≥1且“b≥1”是“a+b≥2”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
为考察高中生的性别与是否喜欢数学课程之间的关系,在湖南某所示范性高中的学生中随机抽取50名学生,得到下表,那么下列判断正确的是( )
参考公式:K2=
,其中n=a+b+c+d;
临界值表:
| 喜欢数学课程 | 不喜欢数学课程 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表:
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
| A、约有5%的把握认为“性别与喜欢数学课程之间有关系” |
| B、约有99%的把握认为“性别与喜欢数学课程之间有关系” |
| C、在犯错误的概率不超过0.050的前提下认为“性别与喜欢数学课程之间有关系” |
| D、在犯错误的概率不超过0.010的前提下认为“性别与喜欢数学课程之间有关系” |
若直线y=x+b与曲线x=
恰有一个公共点,则b的取值范围是( )
| 1-y2 |
| A、-1<b≤1 | ||
| B、-1≤b≤1 | ||
C、-
| ||
D、-1<b≤1或b=-
|
用秦九韶算法计算函数f(x)=12+35x-8x2+79x3+6x4+5x5+3x6当x=-4时的函数值时.v2的值为( )
| A、3 | B、-7 | C、34 | D、-57 |