题目内容
在△ABC中，D为AC中点，点E满足，
=
，若F为边BC上一点，且满足
=λ
，则λ= ．
| BE |
| 2 |
| 5 |
| BD |
| AF |
| AE |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：先根据已知条件用向量
，
表示出
，从而表示出
=
λ
+
λ
，而根据
=
+
，
=μ
，还可用向量
，
表示出
=(1-μ)
+μ
，所以根据平面向量基本定理得到
，解该方程组即得λ的值．
| AB |
| AC |
| AE |
| AF |
| 3 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
| AF |
| AB |
| BF |
| BF |
| BC |
| AB |
| AC |
| AF |
| AB |
| AC |
|
解答：
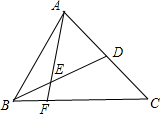
解：如图，根据已知条件得，
=
+
=
+
=
+
[
+
]=
+
；
∴
=
λ
+
λ
；
又
=
+
，B，F，C三点共线；
∴存在μ使
=μ
=-μ
+μ
；
∴
=(1-μ)
+μ
；
∴
，解得λ=
．
故答案为：
．
| AE |
| AB |
| BE |
| AB |
| 2 |
| 5 |
| BD |
| AB |
| 2 |
| 5 |
| BA |
| 1 |
| 2 |
| AC |
| 3 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
∴| AF |
| 3 |
| 5 |
| AB |
| 1 |
| 5 |
| AC |
又
| AF |
| AB |
| BF |
∴存在μ使
| BF |
| BC |
| AB |
| AC |
∴
| AF |
| AB |
| AC |
∴
|
| 5 |
| 4 |
故答案为：
| 5 |
| 4 |
点评：考查向量的加法、减法运算，共线向量基本定理，以及平面向量基本定理．
练习册系列答案
相关题目
不等式
＜0的解集为（ ）
| 7x2-6x-1 |
| x2-x+1 |
| A、空集 | ||
B、{x|-
| ||
C、{x|-1＜x＜
| ||
D、{x|x＜-
|
已知命题p：“?x∈[1，2]，x2-a≥0”，命题q：“?x∈R，x2+2ax+2-a=0”．若命题“p且q”是真命题，则实数a的取值范围为（ ）
| A、-2≤a≤1 |
| B、a≤-2或1≤a≤2 |
| C、a≥1 |
| D、a≤-2或 a=1 |
对正整数n，有抛物线y2=2（2n-1）x，过P（2n，0）任作直线l交抛物线于An，Bn两点，设数列{an}中，a1=-4，且an=
（其中n＞1，n∈N），则数列{an}的前n项和Tn=（ ）
| ||||
| n-1 |
| A、4n |
| B、-4n |
| C、2n（n+1） |
| D、-2n（n+1） |
如图，△BCD所在的平面垂直于正三角形ABC所在的平面，∠BCD=90°，PA⊥平面ABC，DC=BC=2PA，E、F分别为DB、CB的中点．