题目内容
为考察高中生的性别与是否喜欢数学课程之间的关系,在湖南某所示范性高中的学生中随机抽取50名学生,得到下表,那么下列判断正确的是( )
参考公式:K2=
,其中n=a+b+c+d;
临界值表:
| 喜欢数学课程 | 不喜欢数学课程 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表:
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
| A、约有5%的把握认为“性别与喜欢数学课程之间有关系” |
| B、约有99%的把握认为“性别与喜欢数学课程之间有关系” |
| C、在犯错误的概率不超过0.050的前提下认为“性别与喜欢数学课程之间有关系” |
| D、在犯错误的概率不超过0.010的前提下认为“性别与喜欢数学课程之间有关系” |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:根据条件中所给的观测值,同所给的临界值进行比较,根据4.844>3.841,即可得到结论.
解答:
解:由题意,根据表中数据,得到x2=4.844>3.841
由于P(x2≥3.841)≈0.05,
∴在犯错误的概率不超过0.050的前提下认为“性别与喜欢数学课程之间有关系”.
故选:C.
由于P(x2≥3.841)≈0.05,
∴在犯错误的概率不超过0.050的前提下认为“性别与喜欢数学课程之间有关系”.
故选:C.
点评:本题考查独立性检验的应用,解题的关键是正确理解观测值对应的概率的意义.

练习册系列答案
相关题目
由曲线y=x2和直线y=0,x=1,y=
所围成的封闭图形的面积为( )
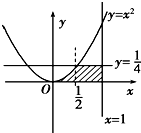
| 1 |
| 4 |

A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=
x3+
x2-tan2θ,其中θ∈(0,
],若g(x)=f′(x),则g′(-1)的取值范围是( )
| cos2θ |
| 6 |
| ||
| 2 |
| 2π |
| 3 |
| A、[-2,2] | ||||
B、[-
| ||||
| C、[-1,2] | ||||
D、[-
|
 如图,△BCD所在的平面垂直于正三角形ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点.
如图,△BCD所在的平面垂直于正三角形ABC所在的平面,∠BCD=90°,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点.