Question

已知边长为

2

的正方形ABCD的对角线BD上任意取一点P，则

PB

•(

PA

+

PC)

的取值范围是（　　）

• A、[0，1]
• B、[0，

  1

  2

  ]
• C、[-4，0]
• D、[-

  1

  2

  ，4]

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：如图所示，建立直角坐标系．利用向量的坐标运算、数量积运算法则、二次函数的单调性即可得出．

解答： 解：如图所示，建立直角坐标系．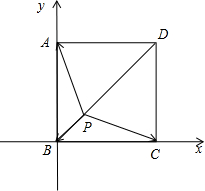
∵点P是边长为

2

的正方形ABCD的对角线BD上任意一点，
可设P（x，x）(0≤x≤

2

)，A(0，

2

)，C(

2

，0)．
∴

PA

=(-x，

2

-x)，

PB

=(-x，-x)，

PC

=(

2

-x，-x)．
∴

PB

•(

PA

+

PC)

=(-x，-x)•(

2

-2x，

2

-2x)
=-2x(

2

-2x)
=4(x-

2

4

)2-

1

2

，
当x=

2

4

时，则

PB

•(

PA

+

PC)

取得最小值-

1

2

；
当x=

2

时，则

PB

•(

PA

+

PC)

取得最大值4．
综上可知：

PB

•(

PA

+

PC)

的取值范围是[-

1

2

，4]．
故选：D．

点评：本题考查了向量的坐标运算、数量积运算法则、二次函数的单调性，属于基础题．