题目内容
下列函数中定义域为[1，+∞）的是（ ）
A、y=
| ||||
B、y=
| ||||
C、y=(
| ||||
| D、y=ln（x-1） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件分别进行判断即可．
解答：
解：A．要使函数有意义，则
，解得x≥1，即函数的定义域为[1，+∞），满足条件．
B．要使函数有意义，则x2-1≥0，解得x≥1或x≤-1，即函数的定义域为[1，+∞）∪（-∞，-1]，不满足条件．
C．函数的定义域为R，不满足条件．
D．要使函数有意义，则x-1＞0，解得x＞1，即函数的定义域为（1，+∞），不满足条件．
故选：A．
|
B．要使函数有意义，则x2-1≥0，解得x≥1或x≤-1，即函数的定义域为[1，+∞）∪（-∞，-1]，不满足条件．
C．函数的定义域为R，不满足条件．
D．要使函数有意义，则x-1＞0，解得x＞1，即函数的定义域为（1，+∞），不满足条件．
故选：A．
点评：本题主要考查函数定义域的求法，要求熟练掌握常见函数成立的条件，比较基础．
练习册系列答案
考前必练系列答案
相关题目
已知全集U=R，集合A={1，2，3，4，5}，B=[3，+∞），则图中阴影部分所表示的集合为（ ）
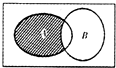
| A、{0，1，2} |
| B、{0，1} |
| C、{1，2} |
| D、{1} |
设全集U=R，集合M={x|-2＜x＜1}，N={x|0＜x＜3}，则N∩（∁UM）等于（ ）
| A、{x|0＜x＜1} |
| B、{x|1≤x＜3} |
| C、{x|-2＜x≤0} |
| D、{x|x≤-2或x≥3} |
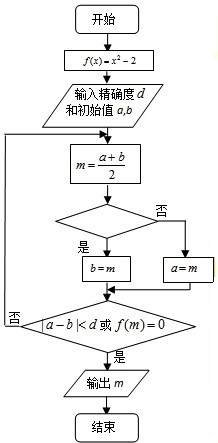如图是用二分法求方程f（x）=0近似解的程序框图，其中f（a）f（b）＜0．判断框内可以填写的内容有如下四个选择：①f（a）f（m）＜0；
②f（a）f（m）＞0；
③f（b）f（m）＜0；
④f（b）f（m）＞0．
其中正确的是（ ）
| A、①③ | B、②③ | C、①④ | D、②④ |
函数f(x)=sin(ωx+φ)(ω＞0，|φ|＜
)的最小正周期为π，若其图象向右平移
个单位后关于y轴对称，则（ ）
| π |
| 2 |
| π |
| 3 |
A、ω=2，φ=
| ||
B、ω=2，φ=
| ||
C、ω=4，φ=
| ||
D、ω=2，φ=-
|
集合A={-1，0，1}，B={y|y=x2+1，x∈A}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、{0，1} | D、{-1，0，1} |
命题p：“?x∈Z，x2≥0”，则?p为（ ）
| A、?x∈Z，x2＜0 |
| B、?x∉Z，x2＜0 |
| C、?x0∈Z，x02≥0 |
| D、?x0∈Z，x02＜0 |