题目内容
下列四个命题:
①定义在[a,b]上的函数y=f(x)在(a,b)内有零点的充要条件是f(a)f(b)<0;
②关于x的方程x2+ax+2=0一根大于1且另一根小于1的充要条件是a<-3;
③直线l1与l2平行的充要条件是l1与l2的斜率相等;
④已知p:椭圆
+2y2=1的焦点在y轴上,q:双曲线
+
=1的焦点在x轴上,当p∧q为真时,实数k的取值范围是(0,
).
其中正确命题的个数为( )
①定义在[a,b]上的函数y=f(x)在(a,b)内有零点的充要条件是f(a)f(b)<0;
②关于x的方程x2+ax+2=0一根大于1且另一根小于1的充要条件是a<-3;
③直线l1与l2平行的充要条件是l1与l2的斜率相等;
④已知p:椭圆
| x2 |
| k-3 |
| x2 |
| 2k |
| y2 |
| k-4 |
| 7 |
| 2 |
其中正确命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:规律型
分析:①根据函数零点存在定理进行判断.
②根据一元二次函数根的分布进行判断即可.
③根据直线平行的充要条件,即可判断.
④根据椭圆和双曲线的定义,以及复合命题的关系即可判断.
②根据一元二次函数根的分布进行判断即可.
③根据直线平行的充要条件,即可判断.
④根据椭圆和双曲线的定义,以及复合命题的关系即可判断.
解答:
解:①定义在[a,b]上的函数y=f(x)在(a,b)内若f(a)f(b)<0,则函数f(x)有零点,反之不一定成立,比如f(x)=|x|在[-1,1]存在零点0,但f(-1)f(1)>0,∴①错误;
②若关于x的方程x2+ax+2=0一根大于1且另一根小于1,则设f(x)=x2+ax+2,则f(1)=3+a<0,即a<-3,∴②正确;
③若l1与l2的斜率相等,则直线l1与l2平行,但l1与l2的倾斜角为90°时,满足两直线平行,但l1与l2的斜率不存在,∴③错误;
④若椭圆
+2y2=1的焦点在y轴上,则0<k-3<
,即3<k<
,若双曲线
+
=1的焦点在x轴上,则
,即0<k<4,
∴当p∧q为真时,p,q同时为真,即
,解得3<k<
,∴实数k的取值范围是(3,
),∴④错误.
故正确的是②,
故选:B.
②若关于x的方程x2+ax+2=0一根大于1且另一根小于1,则设f(x)=x2+ax+2,则f(1)=3+a<0,即a<-3,∴②正确;
③若l1与l2的斜率相等,则直线l1与l2平行,但l1与l2的倾斜角为90°时,满足两直线平行,但l1与l2的斜率不存在,∴③错误;
④若椭圆
| x2 |
| k-3 |
| 1 |
| 2 |
| 7 |
| 2 |
| x2 |
| 2k |
| y2 |
| k-4 |
|
∴当p∧q为真时,p,q同时为真,即
|
| 7 |
| 2 |
| 7 |
| 2 |
故正确的是②,
故选:B.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,考查学生的综合知识的应用.

练习册系列答案
相关题目
设m,n∈R,则“m≥3,n≥3”是“m2+n2≥9”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知全集U=R,集合A={1,2,3,4,5},B=[3,+∞),则图中阴影部分所表示的集合为( )
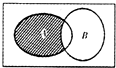

| A、{0,1,2} |
| B、{0,1} |
| C、{1,2} |
| D、{1} |
设全集U=R,集合M={x|-2<x<1},N={x|0<x<3},则N∩(∁UM)等于( )
| A、{x|0<x<1} |
| B、{x|1≤x<3} |
| C、{x|-2<x≤0} |
| D、{x|x≤-2或x≥3} |
函数f(x)=sin(ωx+φ)(ω>0,|φ|<
)的最小正周期为π,若其图象向右平移
个单位后关于y轴对称,则( )
| π |
| 2 |
| π |
| 3 |
A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=4,φ=
| ||
D、ω=2,φ=-
|
设a=30.3,b=log53,c=cos2,则( )
| A、c<b<a |
| B、c<a<b |
| C、a<b<c |
| D、b<c<a |