题目内容
 已知向量
已知向量| a |
| b |
| c |
(Ⅰ)若(3
| a |
| b |
| c |
(Ⅱ)设函数f(x)是
| a |
| b |
考点:平面向量共线(平行)的坐标表示,平面向量数量积的运算
专题:三角函数的图像与性质,平面向量及应用
分析:(Ⅰ)由已知计算3
+4
,由(3
+4
)∥
,求得cosx=sinx,从而得x的值;
(Ⅱ)化简f(x)的解析式,列出f(x)在[0,π]的6个关键点,画出图象即可.
| a |
| b |
| a |
| b |
| c |
(Ⅱ)化简f(x)的解析式,列出f(x)在[0,π]的6个关键点,画出图象即可.
解答:
解:(Ⅰ)由已知,得3
+4
=(7cosx-3sinx,3cosx-sinx);
∵(3
+4
)∥
,又
=(2,1),
∴7cosx-3sinx-2(3cosx-sinx)=0,
化简,得cosx=sinx,
∴tanx=1;
∵x∈[0,π],
∴x=
;
(Ⅱ)∵f(x)=
=(cosx-sinx)cosx+(cosx+sinx)(-sinx)
=cos2x-sin2x-2sinxcosx
=cos2x-sin2x
=
(
cos2x-
sin2x)
=
cos(2x+
),
列表如下: ;
;
∴画出y=f(x)在[0,π]的图象为

| a |
| b |
∵(3
| a |
| b |
| c |
| c |
∴7cosx-3sinx-2(3cosx-sinx)=0,
化简,得cosx=sinx,
∴tanx=1;
∵x∈[0,π],
∴x=
| π |
| 4 |
(Ⅱ)∵f(x)=
| ||||
|
|
=(cosx-sinx)cosx+(cosx+sinx)(-sinx)
=cos2x-sin2x-2sinxcosx
=cos2x-sin2x
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
列表如下:
 ;
;∴画出y=f(x)在[0,π]的图象为

点评:本题考查了向量与三角函数相结合的有关问题,解题时应按照向量的运算法则以及三角函数的知识,进行解答,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
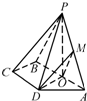 如图,已知四棱锥P-ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO⊥平面ABCD,PO=CD=DA=
如图,已知四棱锥P-ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO⊥平面ABCD,PO=CD=DA=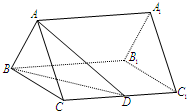 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°. 如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2BC=2CD=2.E为AB中点.现将该梯形沿DE析叠.使四边形BCDE所在的平面与平面ADE垂直.
如图,梯形ABCD中,AB∥CD,∠B=∠C=90°,AB=2BC=2CD=2.E为AB中点.现将该梯形沿DE析叠.使四边形BCDE所在的平面与平面ADE垂直.