题目内容
已知抛物线C:y2=4x的焦点为F.
(1)若点F是线段AP中点,当点A在抛物线C上运动时,求动点P的轨迹方程;
(2)在x轴上是否存在点Q,使得点Q关于直线y=2x的对称点在抛物线C上?如果存在,求所有满足条件的点Q的坐标;如果不存在,请说明理由.
(1)若点F是线段AP中点,当点A在抛物线C上运动时,求动点P的轨迹方程;
(2)在x轴上是否存在点Q,使得点Q关于直线y=2x的对称点在抛物线C上?如果存在,求所有满足条件的点Q的坐标;如果不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设动点P的坐标为(x,y),点A的坐标为(xA,yA),由点F是线段AP中点,得
,由此利用相关点法能求出动点P的轨迹方程.
(2)设点Q的坐标为(t,0).点Q关于直线y=2x的对称点为Q′(x,y),由已知得
.由此能求出存在满足题意的点Q扩其坐标.
|
(2)设点Q的坐标为(t,0).点Q关于直线y=2x的对称点为Q′(x,y),由已知得
|
解答:
解:(1)设动点P的坐标为(x,y),点A的坐标为(xA,yA),
则
=(x-xA,y-yA),
∵F的坐标为(1,0),∴
=(xA-1,yA),
∵点F是线段AP中点,∴(x-xA,y-yA)=-2(xA-1,yA).
解得
,
∵点A在抛物线C上运动,
∴动点P的轨迹方程为:y2=4(2-x)=8-4x.
(2)设点Q的坐标为(t,0).
点Q关于直线y=2x的对称点为Q′(x,y),
则
,解得
.
若Q′在C上,将Q′的坐标代入y2=4x,
得4t2+15t=0,即t=0或t=-
.
∴存在满足题意的点Q,其坐标为(0,0)和(-
,0).
则
| AP |
∵F的坐标为(1,0),∴
| FA |
∵点F是线段AP中点,∴(x-xA,y-yA)=-2(xA-1,yA).
解得
|
∵点A在抛物线C上运动,
∴动点P的轨迹方程为:y2=4(2-x)=8-4x.
(2)设点Q的坐标为(t,0).
点Q关于直线y=2x的对称点为Q′(x,y),
则
|
|
若Q′在C上,将Q′的坐标代入y2=4x,
得4t2+15t=0,即t=0或t=-
| 15 |
| 4 |
∴存在满足题意的点Q,其坐标为(0,0)和(-
| 15 |
| 4 |
点评:本题考查点的轨迹方程的求法,考查满足条件的点的坐标的求法,解题时要认真审题,注意相关点法的合理运用.

练习册系列答案
相关题目
已知x>0,y>0,2x+3y=1,则4x+8y的最小值为( )
| A、8 | ||
| B、6 | ||
C、2
| ||
D、3
|
用总长为120cm的钢条围成一个长方体的框架,要求长方体底面边长比是2:3,当长方体的体积最大时,长方体的高为( )
| A、4cm | B、6cm |
| C、8cm | D、10cm |


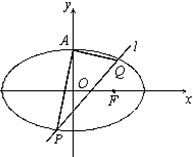 如图,已知椭圆C:
如图,已知椭圆C: