Question

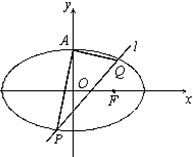如图，已知椭圆C：

x2

a2

+y²=1（a＞1）的上顶点为A，离心率为

6

3

，若不过点A的动直线l与椭圆C相交于P，Q两点，且

AP

•

AQ

=0．
（1）求椭圆C的方程；
（2）若直线AP的斜率为1，求直线PQ的方程；
（3）求证：直线l过定点，并求出该定点N的坐标．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由已知得

a2-1

a

=

6

3

，由此能求出椭圆C的方程．
（2）直线AP的方程为y=x+1，直线AQ的方程为y=-x+1，将y=x+1代入椭圆C的方程

x2

3

+y2=1，得P（-

3

2

，-

1

2

），同理，得Q（

3

2

，-

1

2

）． 由此能求出直线l的方程．
（3）设直线AP的方程为y=kx+1，直线AQ的方程为y=-

1

k

x+1，k≠0，将y=kx+1代入椭圆C的方程，得P（-

6k

1+3k2

，

1-3k2

1+3k2

），同理得Q（

6k

k2+3

，

k2-3

k2+3

），由此求出直线l的方程为y=

4k2-1

4k

x-

1

2

．从而能证明直线l过定点N（0，-

1

2

）．

解答： （1）解：∵椭圆C：

x2

a2

+y²=1（a＞1）的上顶点为A，离心率为

6

3

，
∴

a2-1

a

=

6

3

，解得a²=3，
∴椭圆C的方程为

x2

3

+y2=1．
（2）解：由

AP

•

AQ

=0，知AP⊥AQ，从而直线AP与坐标轴不垂直，
由A（0，1），直线AP的斜率为1，得直线AP的方程为y=x+1，直线AQ的方程为y=-x+1，
将y=x+1代入椭圆C的方程

x2

3

+y2=1，并整理得：4x²+6x=0，
解得x=0或x=-

3

2

，因此P的坐标为（-

3

2

，-

1

2

），同理，得Q（

3

2

，-

1

2

）．
直线l的方程为y=-

1

2

．
（3）证明：由

AP

•

AQ

=0，知AP⊥AQ，从而直线AP与坐标轴不垂直，
由A（0，1）可设直线AP的方程为y=kx+1，直线AQ的方程为y=-

1

k

x+1，k≠0，
将y=kx+1代入椭圆C的方程

x2

3

+y2=1，并整理得：（1+3k²）x²+6kx=0，
解得x=0或x=-

6k

1+3k2

，因此P的坐标为（-

6k

1+3k2

，-

6k2

1+3k2

+1），
即（-

6k

1+3k2

，

1-3k2

1+3k2

），
将上式中的k换成-

1

k

，得Q（

6k

k2+3

，

k2-3

k2+3

），
直线l的方程为：y=

k2-3 k2+3 - 1-3k2 1+3k2

6k k2+3 + 6k 1+3k2

（x-

6k

k2+3

）+

k2-3

k2+3

，
化简得直线l的方程为y=

4k2-1

4k

x-

1

2

．
因此直线l过定点N（0，-

1

2

）．

点评：本题考查椭圆方程的求法，考查直线方程的求法，考查直线过定点坐标的证明，解题时要认真审题，注意函数与方程思想的合理运用．