题目内容
20.对正整数m的3次幂有如下分解方式:13=1 23=3+5 33=7+9+11 43=13+15+17+19
根据上述分解规律,则103的分解中最大的数是131.
分析 由23=3+5,33=7+9+11,43=13+15+17+19,按以上规律分解,第n个式子可以表示为(n+1)3=(n2+n+1)+(n2+n+3)+…+(n2+3n+1)
解答 解:由13=1,23=3+5,33=7+9+11,43=13+15+17+19,
可得53=21+23+25+27+29,
注意观察各个数分解时的特点,不难发现:当底数是2时,可以分解成两个连续的奇数之和;当底数是3时,可以分解成三个连续的奇数之和.
按以上规律分解,第n个式子的第一个和式是n(n+1)+1,一共有n+1项.
∴第n个式子可以表示为:(n+1)3=(n2+n+1)+(n2+n+3)+…+(n2+3n+1),
∴则103的分解中最大的数是102+3×10+1=131,
故答案为:131.
点评 本题考查归纳推理,求解的关键是根据归纳推理的原理归纳出结论,其中分析出分解式中项数及每个式子中各数据之间的变化规律是解答的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
19.设a>b,则下列不等式中正确的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | a+c>b+c | C. | ac2>bc2 | D. | a2>b2 |
8.等差数列3,1,-1,-3,…,-93的项数为( )
| A. | 52 | B. | 51 | C. | 49 | D. | 50 |
12.已知正方形ABCD的对角线相交于点O,若随机向此正方形内投放一颗豆子,则它落在△AOB内的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
9.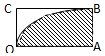 如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
 如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )
如图,长方形的四个顶点坐标为O(0,0),A(4,0),B(4,2),C(0,2),曲线y=$\sqrt{x}$经过点B,现将质点随机投入长方形OABC中,则质点落在图中阴影部分的概率为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
10.已知等比数列{an}中的各项都是正数,且${a_1},\frac{1}{2}{a_3},2{a_2}$成等差数列,则$\frac{{{a_9}+{a_{10}}+{a_{13}}}}{{{a_7}+{a_8}+{a_{11}}}}$=( )
| A. | $1+\sqrt{2}$ | B. | $1-\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3-2\sqrt{2}$ |
 已知:四棱锥P-ABCD的底面为直角梯形,且AB∥CD,△DAB=90°,DC=2AD=2AB,侧面PAD与底面垂直,PA=PD,点M为侧棱PC上一点D.
已知:四棱锥P-ABCD的底面为直角梯形,且AB∥CD,△DAB=90°,DC=2AD=2AB,侧面PAD与底面垂直,PA=PD,点M为侧棱PC上一点D. 某种平面分形如图所示,以及分形图是有一点出发的三条线段,二级分形图是在一级分形图的每条线段的末端出发在生成两条线段,…,依次规律得到n级分形图,那么n级分形图中共有3•2n-3条线段.
某种平面分形如图所示,以及分形图是有一点出发的三条线段,二级分形图是在一级分形图的每条线段的末端出发在生成两条线段,…,依次规律得到n级分形图,那么n级分形图中共有3•2n-3条线段.